MainPage/Algorithm&DataStructures/Lecture

Lecture 1

Представьте, что:

• браузер загружает страницы и видео в 3-4 раза медленнее обычного
• оплата по кредитной карте в магазине занимает 10-15 минут
• чтобы набрать букву в СМС-ке смартфону требуется 5 секунд
• И т.д. и т.П.
• Вот что может произойти если пользоваться неэффективными алгоритмами!

想象一下：

• 浏览器加载页面和视频的速度比正常情况慢 3-4 倍
• 在店内用信用卡付款需要 10-15 分钟
• 智能手机在短信中输入一个字母需要 5 秒
• 等等。 如果您使用低效算法，就会发生这种情况！

Рассмотрим задачу:

• Время работы алгоритма 1 пропорционально функции f= N2
• Время работы алгоритма 2 пропорционально функции f= NlogN Есть два компьютера
• Компьютер А выполняет 10° операций в секунду (частота ~ ГГЦ)
• Компьютер Б выполняет 106 операций в секунду (частота ~ МГЦ)

考虑问题：

• 算法 1 的运行时间与函数 $f= N^2$ 成正比
• 算法 2 的运行时间与函数 $f= N\log N$ 成正比 有两台电脑
• 计算机 A 每秒执行 $10^9$ 操作（频率～GHz）
• 计算机 B 每秒执行 $10^6$ 次操作（频率～MHz）

Мало ядер? Закон Амдала

В каких единицах лучше измерять время работы алгоритма?

• Важно сравнивать алгоритмы между собой
• От чего зависит время работы (реализации) алгоритма?
• От N- мера размера задачи
• От входных данных
• От платформы исполнения
• От языка программирования и компилятора
• Время выполнения ~ число выполненных операций (строк кода)
• Что такое одна операция?

衡量算法运行时间的最佳单位是什么？

• 相互比较算法很重要
• 什么决定了算法的运行时间（实现）？
• 来自任务大小的 N 度量
• 来自输入
• 从执行平台
• 来自编程语言和编译器
• 执行时间～执行的操作数（代码行数）
• 什么是一次操作？

Какой из алгоритмов лучше?

• f.(N) = 239 x N2 + 30 × N + 566
• fa(N) = 10 x N3
• При маленьких N? При больших N?
• Постоянные множители будут варьироваться в зависимости от языка программирования, компилятора, архитектуры компьютера…
• f(N) - это какое время?

哪种算法更好？

• f.(N) = 239 x N2 + 30 x N + 566
• fa(N) = 10 x N3

-对于小 N？ 对于大 N? -常数乘数会有所不同，具体取决于 取决于编程语言、编译器、计算机体系结构…… -f (N) 是什么时间？

void insertion_sort(int *a, int n)
{
    int i, j, t;
    for (i=1; i < n; ++i) {
        t = a[i];
        j = i;
        while (j > 0 && a[j-1] > t) {
            a[j] = a[j-1];
            --j;
        }
        a[j]=t;
    }
}

Инвариант: в начале каждого цикла for подмассив а[0..i-1] состоит из отсортированных элементов изначального подмассива а[0..i-1]
不变性：在每个 for 循环的开始，子数组 a[0..i-1] 由原始子数组 a[0..i-1] 的排序元素组成

Среднее время работы

• Дает среднее время выполнения при определенных предположениях о частоте появления того или иного входа
• Требует знания предметной области

Наихудшее время работы

• Дает верхнюю оценку времени выполнения вне зависимости от входных данных
• Не требует знания предметной области
• Позволяет гарантировать время выполнения
• Легче рассчитывается
• Среднее часто ведет себя как наихудшее

平均运行时间

• 在特定输入发生频率的某些假设下给出平均执行时间
• 需要领域知识 最差运行时间
• 无论输入数据如何，都给出执行时间的上限估计
• 不需要领域知识
• 让你保证执行时间
• 更容易计算
• 平均通常表现得像最差的

Пренебрежем постоянными множителями, членами меньшего порядка и сфокусируемся на больших /

• Математически много проще :)
• Непонятно как считать постоянные множители
• На самом деле почти ничего не теряем!
• На маленьких задачах и так все быстро (тут постоянные множители важны!)
• Закон Мура <-> вычислительные потребности

Время работы f() пропорционально:

• $1、\log N、N、N\log N、N^2、N^3、2^N$
• Насколько увеличится $f(N)$ при $N\to2N$?

我们忽略常数因子、低阶项并关注大 N

• 数学上更容易 :)
• 不清楚如何计算常数因子
• 事实上，我们几乎没有损失！
• 在小任务上一切都很快（常数乘数在这里很重要！）
• 摩尔定律 <-> 计算需求

$f()$ 的运行时间正比于：

• $1、\log N、N、N\log N、N^2、N^3、2^N$
• 当 $N\to2N$ 时，$f(N)$ 会增加多少？

Лучший алгоритм ~ наихудшее время работы алгоритма? растет наиболее медленно с увеличением размера входной задачи (т.е. смотрим только на порядок роста) Цель - линейный рост Какой из алгоритмов лучше?

• $f_1(N) = 239 x N^2 + 30 \times N + 566$
• $f_2(N) = 10 x N^3$
  • $f_1(30) = 216 566; f_2(30) = 270 000$
  • $f_1(100) = 2 393 566; f_2(100) = 10\ 000\ 000$
  • $f_1(1000) = ???; f_2(1000) = ???$

Что лучше: $N^{100}$ или $2^N$? $N = 1000$?

最佳算法～最差算法时间？ 随着输入问题规模的增加，增长最慢（即只看增长顺序） 目标 - 线性增长 哪种算法更好？

• $f_1(N) = 239 x N^2 + 30 \times N + 566$
• $f_2(N) = 10 x N^3$
  • $f_1(30) = 216 566; f_2(30) = 270 000$
  • $f_1(100) = 2 393 566; f_2(100) = 10\ 000\ 000$
  • $f_1(1000) = ???; f_2(1000) = ???$

哪个更好：$N^{100}$ 或 $2^N$？ $N = 1000$？

А как нам описать время выполнения безотносительно ко входным данным, а не только в (наихудшем случае?
我们如何描述执行时间而不考虑输入数据，而不仅仅是（最坏的情况？

О-обозначения: асимптотическая верхняя граница
Говорим, что $f(N)= O(g(N))$, ecли $\exist c$ и $N_0 > 0$ такие, что $0 \le f(N) \le cg(N)$ для всех $N\ge N_0$

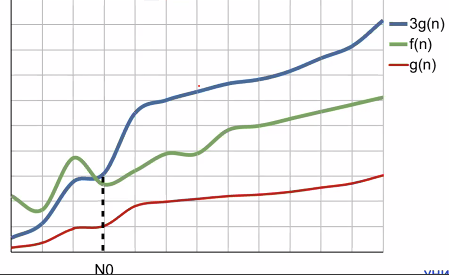
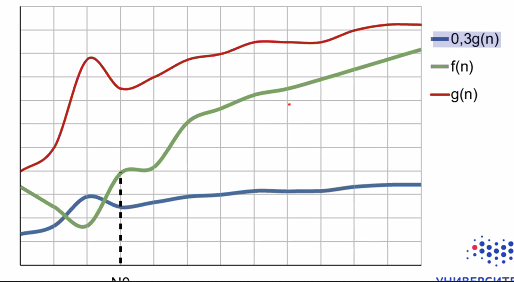
($\Omega$-обозначения: асимптотическая нижняя граница Говорим, что f(N) = Q(9 (N)), если 3 си N > 0 такие, что 0 5 cg (N) = f(N) для всех N ≥ No -0,3g(n)

Пусть есть функция f(N) = 239 × N2 + 30 × N + 566 Что верно?

• f(N) = O(N)
• f(N) = O (N2)
• f(N) = 2 (N)
• f(N) = 0 (N2)
• f(N) = O (N3) Как можно выразить постоянную функцию?

设函数 f(N) = 239 × N2 + 30 × N + 566 什么是对的？

• f(N) = O(N) -
• f(N) = O(N2) +
• f(N) = 2(N) +
• f(N) = 0 (N2) +
• f(N) = O(N3) + 如何表达一个常量函数？

a f(N) = ax NK + ax-1 NK-1 + … + agNt ao

• Докажем, что f(N) = O (NK), т.е. можно пренебречь постоянными множителями и членами меньшего порядка a f(N) = a NK + ax. 1 NK-1 + … + ag N+ ao ≤ SladNK+|ax-1|NK-1+…+|aj|N+|a0l5
• Возьмем с = lakl + |ax-1l + .. + |ag| + | aol, No = 1, тогда F(N) ≤ CNK для всех N≥ No

void insertion_sort(int *a, int n)
{
    int i, j, t;
    for (i=1; i < n; ++i) {
        t = a[i];
        j = i;
        while (j > 0 && a[j-1] > t) {
            a[j] = a[j-1];
            --j;
        }
        a[j]=t;
    }
}

T() = O(N2) - верхняя граница для наихудшего случая T() = Q (N) - нижняя граница для наилучшего случая Верно ли, что S2 (N2) - время работы в наихудшем случае?

Экспонента vs полином

Покажем, что $2^N$ растет быстрее $N^2\Leftrightarrow2N \ne O (N^2)$

• $N^2 < 2^N$ для всех $N ≥ 5$. По индукции:
  • База: $5^2 = 25 < 2^5 = 32$
  • Шаг индукции: пусть $k^2 < 2^k$, надо показать, что $(k + 1)^2 < 2^{k+1} = 2 \cdot 2^k$
  • По индукционному предположению $2k^2 < 2 \cdot 2^k$=> достаточно показать, что $(k + 1)^2 < 2k^2$
  • $(k+1)/k<\sqrt{2}\Leftrightarrow 1/k<\sqrt{2}-1\Leftrightarrow k*>1/（\sqrt{2}-1）\approx 2.4$
  • Т.о. для всех $k > 5$ шаг индукции выполняется
• Покажем, что $2^N$ растет быстрее $N^k\Leftrightarrow 2^N\ne O(N^k)$
• $N^k < 2^N$ для всех $N ≥ N_0$. По индукции по $k$ для достаточно больших $N$:
  • База $k = 1: 2^N > N^2 > N$ для всех $N > N_0 = 5$
  • Шаг индукции: пусть $N^k < 2^N$, надо показать, что $N^{k+ 1}< 2^N$ для достаточно больших $N$
  • $N^k\cdot4^k<2^N.4^k\Leftrightarrow (4N)^K < 2^{N+ 2K}$
  • Переоброзначим $M =4N:M^k*<2^{M/4+2k}$ для $M^k<2^{M/2}$
  • $2^{M/4 +2k} < 2^{M/2}$ для всех $M > 8k \Leftrightarrow M^k < 2^{M/2}$
  • T.O. $N^{k+ 1} = N^k\cdot N < 2^{N/2}\cdot 2^{N/2} = 2^N$ для достаточно больших $N$

$N^x$ растет быстрее, чем $(\log N)^y$ для $х, у > 0$ и достаточно больших $N \Leftrightarrow N^x \ne O((\log N)^y)$

• Переобозначим $M = \log N \Leftrightarrow N = 2^M$ :
  • Вместо полинома получим показательную функцию, вместо полилогарифма - степенную
  • Надо показать, что $2^{xM} \ne O(M^y)$
• Знаем, что $2^M \ne O (M^y) => 2^{xM} ne O(M^y)$

Lecture 2

Принцип divide-and-conquer

• Решаем задачу рекурсивно, применяя на каждом уровне рекурсии три шага:
• Divide: разделяем задачу на несколько таких же задач меньшего размера
• Conquer: решаем подзадачи рекурсивно
  • Подзадачи малого размера решаем прямым решением
• Combine: комбинируем решения подзадач в решение исходной задачи

Оценка сложности

• $T(N) = T (N/2) + T (N/2) + 1$, где $T (N)$ - время выполнения задачи размера $N$

• Какая сложность?

• Метод №1 - сделаем предположение и докажем его корректность
• По индукции: $T(N) < cN$ для некоторой константы $с$
  • Более строгое предположение: $T(N) ≤ cN-a, a≥ 1$
  • База индукции: $T(1) < c - а$
  • Шаг индукции: пусть $T(N /2) ≤ cN/2 - а$, надо показать, что T(N) \le cN - a
  • $T(N) = T(N/2) + T(N/2) + 1 ≤ cN - 2a + 1 ≤ cN-a, a ≥ 1$

• Как угадать решение?

• На нижнем уровне $N$ узлов (подзадач) каждая со временем выполнения $Т(1)$, поэтому время работы этого уровня $O (N)$
• Общее время работы:
  • $1+2^1+2^2+\cdots+2^{\log N-1}+O(N)=$
  • $=(2^{\log N}-1)/(2-1)+O(N)=N-1+O(N)$
• $T(N)=O(N)$
• Предположение: количество элементов в исходной задаче равно степени двойки
  • Не влияет на порядок роста: почему?

Дерево рекурсии

• Рекурсия останавливается, когда размер подзадачи станет равным единице

Умножение чисел

• Требуется перемножить два $n$ -значных числа
• В столбик? Оценка сложности: $0 (N^2)$
• Divide: разобьем каждое число на две $п /2$ -значные половины
• $num_1 = x_1 \cdot 10^{n/2} + x_0$
• $num_2 = y_1 \cdot 10^{n/2} + Y_0$
• Conquer: HaaeM $x_1 \cdot y_1= ; x_1 \cdot y_0; x_0 \cdot y_1 ; x_0 \cdot y_0$
• Произведение однозначных чисел выполняется за $О (1)$

• Combine: $num_1 \cdot num_2 = (x_1 \cdot 10^{n/2} + x_0)(y_1 \cdot 10^{n/2} + y_0) = x_1\cdot y_1 \cdot 10^n +(x_1 \cdot y_0 + x_0 \cdot y_1) \cdot 10^{n/2} + x_0 * y_0$

• $x_1\cdot y_1\cdot 10^n+(x_1y_0+x_oy_1）\cdot 10^{n/2}+x_0\cdot y_0$
• Предположим, что:
  • Умножение на $10^n$ делаем сдвигом цифр в массиве => $0 (N)$
  • Сложение делаем поразрядно с переносом. Разрядность цифр в формуле не превосходит $2N => O (N)$
• $ T(N) = 4T(N/2) + O(N)$
• $T(N)=O(？）$

Рекурсивное умножение

• Каждая цифра из $num_1$, перемножается с каждой цифрой из $num^2 => N^2$ операций на нижнем уровне

• $T(N) = N(2^{\log N+1}-1)/(2-1) = N(2N - 1) =O (N^2)$

Алгоритм Карацубы

• Divide: как и прежде
• Conquer: вместо четырех подзадач требуется решить три
• $A=x_1\cdot y_1$
• $B=x_0\cdot y_0$
• $C=(x_1+x_0)(y_0+y_1)$
• Combine: $num_1 \cdot num_2 = A\cdot 10^n+(C-A-8)\cdot 10^{n/2}+B$
• $C-A-B=(x_1+x_0)(y_0+y_1)-x_1\cdot y_1-x_0\cdot y_0$
• $T(N)=3T(N/2)+O(N)$
• $T(N)=O(?)$