MainPage/Computatioonal&Mathematics/Test

Каталог

• Контрольная работа 1
  • Вариант 1
  • Вариант 2
  • Вариант 3
  • Вариант 4
  • Вариант 5
  • Вариант 6
  • Вариант 7
  • Вариант 8
  • Вариант 9
  • Вариант 10
  • Вариант 11
  • Вариант 12
  • Вариант 13
  • Вариант 14
  • Вариант 15

Контрольная работа 1

Вариант 1

1. Вычислить интеграл методом Симпсона. Оценить погрешность вычислений:
   用辛普森法计算积分。 估计计算误差：

   \[\int^4_0(6x^2+8x){\rm d}x\qquad(n=10)\]

2. Решить систему уравнений методом Гаусса-Зейделя, выполнить 4 итерации:
   使用 Gauss-Seidel 方法求解方程组，执行 4 次迭代：

   \[A=\begin{pmatrix} 1.9 & 6.7 & -2.5\\ 10.4 & -3.6 & -2.7\\ 0.9 & 1.3 & 4.3\\ \end{pmatrix} \qquad B=\begin{pmatrix} 2.1\\ -7.9\\ 3.5\\ \end{pmatrix}\]
3. Написать программу решения нелинейного уравнения $x^3 + 4x − 6 = 0$ методом половинного деления с точностью до $0.01$ на интервале $[0, 2]$.
   编写一个程序，通过二分法在区间 $[0, 2]$ 上求解非线性方程 $x^3 + 4x − 6 = 0$，精度为 $0.01$。

4. Что такое правило Рунге?
   什么是朗格规则？ Правило Рунге - это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений, проводимых с разными шагами $h$:
   朗格规则是一种根据比较不同步骤 $h$ 执行的计算结果来估计误差的经验方法：

   \[I - I_{h/2}\approx\frac{I_{h/2}-I_h}{2^k-1}\]

   где 其中：

   • $I$ – точное значение интеграла;
     $I$ - 积分的精确值；
   • $I_{h/2}$, $I_h$ - приближенные значения интеграла, вычисленные с различными шагами $h$;
     $I_{h/2}$, $I_h$ - 不同步长计算的积分的近似值 $h$；
   • $k$ - порядок точности квадратурной формулы, ($𝑘=2$ - для формул средних прямоугольников и трапеций, $𝑘=4$ - для формулы Симпсона).
     $k$ - 求积公式的精度顺序，($𝑘=2$ - 对于中长方形和梯形的公式，$𝑘=4$ - 对于辛普森公式)。

5. Что такое скорость сходимости численного метода?
   什么是数值方法的收敛速度？

   Скорость сходимости (эффективность) – обозначает количество итераций, затраченных алгоритмом для достижения приемлемой точности решения задачи. Чем выше скорость, тем меньше итераций необходимо выполнить.
   收敛率（效率）——表示算法为达到解决问题的可接受精度所花费的迭代次数。 速度越高，需要执行的迭代越少。

   Различают линейную, сверхлинейную, квадратичную скорость:
   有线性、超线性、二次速度：

   \[\lvert x^n-x^\ast\rvert\le\alpha\lvert x^{n-1}-x^\ast\rvert^\beta, \alpha\in(0,1)\]
   • $\beta=1$ - линейная
   • $1<\beta<2$ - сверхлинейная
   • $\beta = 2$ - квадратичная

Вариант 2

1. Вычислить интеграл методами прямоугольников (всех) и написать программу метода трапеций:

\[\int^2_0(4x^2-5x) {\rm d}x\qquad(n=10)\]

1. Решить систему уравнений методом простой итерации, выполнить 4 итерации:

\[A=\begin{pmatrix} 5.2 & 1.2 & 1.5\\ 3.1 & -2.5 & -9.8\\ 0.4 & 2.3 & 1.2\\ \end{pmatrix}\qquad B=\begin{pmatrix} 2.0\\ -3.5\\ 1.2\\ \end{pmatrix}\]

1. Написать программу нахождения корня нелинейного уравнения $x^3 − 2x^2 + 4 = 0$ методом простой итерации с точностью до $0.01$ на интервале $[-2, 0]$.
2. Какое приближенное значение корня уравнения $9x^3 − 3x^2 − 8x − 2 = 0$ Вы получите на четвертом шаге метода половинного деления, если начальный отрезок локализации есть $[0;2]$? В ответ запишите приближенное значение корня с точностью $10^{−3}$. Шаги отсчитываем с первого?
3. Выведите формулу трапеций для численного вычисления определенного интервала.

Вариант 3

1. Вычислить интеграл методом трапеций. Оценить погрешность вычислений:

\[\int^3_0(2x^2+5x-10) {\rm d}x\qquad(n=10)\]

1. Решить систему нелинейных уравнений методом Ньютона с точностью до 0.01, принимая начальные приближения $x_0=1, y_0=1$:

\[\begin{cases} x-3y^2=-2\\ 5x^2+2y^2=10 \end{cases}\]

1. Написать программу и найти корень нелинейного уравнения $x^3 − 3x + 9x + 4 = 0$ секущих с точностью до $0.01$ на интервале $[-2, 0]$.
2. Имеет ли место сходимость к найденному корню $x^\ast = 0.2304$ уравнения $2𝑥 + \lg(2𝑥 + 3) = 1$, если $\lambda=-0.4$ и $𝑥_0 = 0$?

3. Приведите графическую интерпретацию метода касательных. Метод Ньютона (касательных)

   

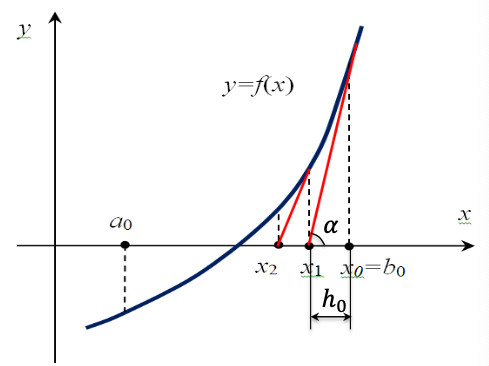
   Идея метода: функция $y = f(x)$ на отрезке $[a, b]$ заменяется касательной и в качестве приближенного значения корня
   方法思想：将线段 $[a,b]$ 上的函数 $y = f(x)$ 替换为切线并作为根的近似值

   $x^\ast = x_n$ принимается точка пересечения касательной с осью абсцисс.
   $x^\ast = x_n$ 取切线与横坐标轴的交点。

   $x_1 = x_0 - h_0$

   $h_0 = \frac{f(x_0)}{\tan\alpha} = \frac{f(x_0)}{f’(x_0)}$

   $x_1 = x_0 - \frac{f(x_0)}{f’(x_0)}$

   Рабочая формула метода:
   该方法的工作公式：

   \[x_i=x_{i-1}-\frac{f(x_{i-1})}{f'(x_{i-1})}\]

   Критерий окончания итерационного процесса:
   迭代过程结束的标准：

   $\lvert x_n-x_{n-1}\rvert\le\varepsilon$ или $\lvert\frac{f(x_n)}{f’(x_n)}\rvert\le\varepsilon$ или $\lvert f(x_n)\rvert\le\varepsilon$

   Приближенное значение корня: $x^\ast= x_n$
   根的近似值：$x^\ast= x_n$

Вариант 4

1. Вычислить интеграл методом Симпсона. Оценить погрешность вычислений:

\[\int^4_0(4x^2+3x-7) {\rm d}x\qquad(n=10)\]

1. Написать программу решения системы нелинейных уравнений методом простой итерации с точностью до $0.01$, принимая начальные приближения $x_0 = 0.5, y_0 = 1$:

\[\begin{cases} y-0.8x^2+x=1.5\\ 2x+y-\frac{1}{4}y^3=1.7\\ \end{cases}\]

1. Написать программу и найти корень нелинейного уравнения $2x^3 + 4x − 7 = 0$ методом половинного деления с точностью до $0.01$ на интервале $[2, 4]$.
2. Как вычислить определенный интеграл по формуле Ньютона-Котеса?
3. Приведите графическую интерпретацию метода простой итерации для решения нелинейного уравнения при сходящемся процессе.

Вариант 5

1. Вычислить интеграл методами прямоугольников (всех):

\[\int^2_0(4x^2-5x){\rm d}x\qquad(n=10)\]

1. Написать программу решения системы нелинейных уравнений методом Ньютона с точностью до $0.01$, принимая начальные приближения $x_0 = 0.5, y_0 = −1$:

\[\begin{cases} \sin(2x-y)-1.2x=0.4\\ x^2+2y^2=1\\ \end{cases}\]

1. Написать программу и найти корень нелинейного уравнения $3x^3 − 2x^2 + 1 = 0$ методом простой итерации с точностью до $0.01$ на интервале $[-1, 0]$.
2. Имеет ли место сходимость к найденному корню $x^\ast = 0.2304$ уравнения $2x + \lg(2x + 3) = 1$, если $\lambda=0.4$ и $𝑥_0 = 0$?

3. При каком условии метод Гаусса-Зейделя будет сходиться к решению задачи?
   Теорема. Достаточным условием сходимости итерационного процесса к решению системы при любом начальном векторе $x_i^{(0)}$ является выполнение условия преобладания диагональных элементов или доминирование диагонали:
   定理：对于任何初始向量 $x_i^{(0)}$ ，迭代过程收敛到系统解的充分条件是满足对角线元素普遍存在或对角线优势的条件：

   \[\lvert a_{ii}\rvert\ge\sum_{j\ne i}\lvert a_{ij}\rvert,\qquad i=1,2,\cdots,n\]

   При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т. е. для некоторых систем итерации сходятся и при нарушении этого условия.
   此外，对于至少一个方程，必须严格满足不等式。 这些条件对于该方法的收敛是充分的，但它们不是必需的，即对于某些系统，即使违反此条件，迭代也会收敛。

   Теорема. Достаточным условием сходимости итерационного метода к решению системы при любом начальном векторе $x_i^{(0)}$ является требование к норме матрицы $C$:
   定理。 迭代法收敛于系统对任意初始向量 $x_i^{(0)}$ 的充分条件是对矩阵 $C$ 范数的要求：

   \[\lVert C\rVert < 1\] \[\lVert C\rVert=\max_{1\le i\le n}\sum_{j=1}^n\lvert c_{ij}\rvert < 1\] \[\lVert C\rVert=\max_{1\le j\le n}\sum_{i=1}^n\lvert c_{ij}\rvert < 1\] \[\lVert C\rVert=\sqrt{\sum_{i=1}^n\sum_{j=1}^n c_{ij}^2}<1\]

   Условие сходимости $\lVert C\rVert < 1$ в этом методе равносильно условию диагонального преобладания.
   该方法中的收敛条件 $\lVert C\rVert < 1$ 等同于对角优势条件。

Вариант 6

1. 编写程序，在区间 $[-2, 0]$ 上用牛顿法求非线性方程 $3x^3-3x^2+3.5=0$ 的根，精度为0.01.

2. Что такое численное интегрирование? В каких случаях оно применяется?
   什么是数值积分？ 在什么情况下适用？

   当牛顿-莱布尼茨公式不可能或难以使用时(Когда формулой Ньютона –Лейбница невозможно или затруднительно воспользоваться: )：

   • подынтегральная функция представлена в виде таблицы значений или задана графически, тогда первообразная $F(x)$ не существует;
     被积函数以数值表形式呈现或以图形方式给出，则反导数 $F(x)$ 不存在；
   • подынтегральная функции имеет сложное аналитическое выражение или/и её первообразная не выражается через элементарные функции или слишком громоздка.
     被积函数具有复杂的解析表达式和/或其反导数不能用初等函数表示或过于繁琐。

   Тогда применяют численное (приближенное) интегрирование.
   然后使用数值（近似）积分。

3. Имеет ли место сходимость к найденному корню 𝑥∗ = −0,3796 уравнения $x^3-2x^2+7x+3=0$, если $\lambda=0.07$ и $x_0 = 0$?
   如果 $\lambda=-0.07$ 且 $𝑥_0 = 0$ ，方程 $x^3-2x^2+7x+3=0$, 是否收敛到找到的根 $x^\ast = -0.3796$ ?

Вариант 7

1. 编写程序求非线性方程 $x^3-3x^2+1.5=0$ 的根,通过二分法在区间 $[2, 4]$ 上精度为 $0.01$。

2. Что такое сходимость численного метода?
   什么是数值方法的收敛性？

   Численное решение задачи должно стремиться к точному решению задачи.
   问题的数值解应该趋向于问题的精确解。

   Алгоритм сходится, если последовательность приближений
   算法收敛，如果近似序列

   \[x_1,x_2,\cdots,x_n\to x^\ast, n\to\infty,\lim_{n\to\infty}x_n=x^\ast\]

3. От чего зависит точность численного интегрирование?
   什么决定了数值积分的精度？

   Погрешность численного интегрирования определяется шагом разбиения. Уменьшая этот шаг, можно добиться большей точности.
   数值积分的误差由分割步长决定。通过减少这一步，您可以获得更高的准确性。

Вариант 8

1. Написать программу и найти корень нелинейного уравнения $x^3 − 3x^2 + 1.5 = 0$ методом половинного деления с точностью до $0.01$ на интервале $[2, 4]$.
   编写程序，在区间 $[-2, 0]$ 上用牛顿法求非线性方程 $7x^2 + 4x - 5 = 0$ 的根，精度为 $0.01$。

2. Имеет ли место сходимость к найденному корню $x^\ast = 22.7598$ уравнения $\ln(x − 5) \sin x + 2$, если $\lambda=0.6$ и $x_0 = 23$?
   如果 $\lambda=0.6$ 且 $x_0 = 23$ ，方程 $ln(x-2)\sin x+2$, 是否收敛到找到的根 $x^\ast = 22.7598$ ?

3. Что такое сходимость численного метода?
   什么是数值方法的收敛性？

   收敛性是当离散化参数趋于零时，方法的解的值对原问题的解的对应值的趋势
   Скорость сходимости (эффективность) – обозначает количество итераций, затраченных алгоритмом для достижения приемлемой точности решения задачи. Чем выше скорость, тем меньше итераций необходимо выполнить.

Вариант 9

1. 编写程序，在区间 $[-2, 0]$ 上使用精度为 $0.01$ 的正割法求非线性方程 $2x^3 + 9x^2 − 4 = 0$ 的根。

2. Основные показатели численных методов.数值方法的主要指标。
   Основные требования и показатели численных методов:
   数值方法的基本要求和指标:

   • устойчивость; 稳定;
   • сходимость; 收敛;
   • эффективность (скорость сходимости); 效率（收敛速度）；

   Алгоритм считается устойчивым, если он обеспечивает нахождение существующего и единственного решения при различных исходных данных
   如果算法为各种输入提供现有且唯一的解决方案，则该算法被认为是稳定的。

   Скорость сходимости (эффективность) – обозначает количество итераций, затраченных алгоритмом для достижения приемлемой точности решения задачи. Чем выше скорость, тем меньше итераций необходимо выполнить.
   收敛率（效率）——表示算法为达到解决问题的可接受精度所花费的迭代次数。 速度越高，需要执行的迭代越少。

3. В каких случаях применяют численное интегрирование?
   什么情况下用到数值积分？

   Когда формулой Ньютона–Лейбница невозможно или затруднительно воспользоваться:
   当牛顿-莱布尼茨公式不可能或难以使用时：

   • подынтегральная функция представлена в виде таблицы значений или задана графически, тогда первообразная $F(x)$ не существует;
     被积函数以数值表形式呈现或以图形方式给出，则反导数 $F(x)$ 不存在；
   • подынтегральная функции имеет сложное аналитическое выражение или/и её первообразная не выражается через элементарные функции или слишком громоздка.
     被积函数具有复杂的解析表达式和/或其反导数不能用初等函数表示或过于繁琐。

   Тогда применяют численное (приближенное) интегрирование.
   然后使用数值（近似）积分。

Вариант 10

1. 编写程序，在区间 $[2, 4]$ 上用精度为 $0.01$ 的半除法求非线性方程 $5x − e^x + 7 = 0$ 的根。
2. 什么是朗格法则？(Что такое правило Рунге?)
3. 如果 $\lambda=-0.07$ 且 $𝑥_0 = 0$ ，方程 $x^3-2x^2+7x+3=0$, 是否收敛到找到的根 $x^\ast = -0.3796$ ?

   Вариант 11

   Вариант 12

   Вариант 13

   Вариант 14

   Вариант 15