MainPage/Discrete Mathematics/Домашнее Задание 5

Вариант №122

V/V	$e_1$	$e_2$	$e_3$	$e_4$	$e_5$	$e_6$	$e_7$	$e_8$	$e_9$	$e_{10}$	$e_{11}$	$e_{12}$	p(e)
$e_1$	0		1	1	1		1			1	1		6
$e_2$		0	1	1	1			1					4
$e_3$	1	1	0	1	1		1		1	1			7
$e_4$	1	1	1	0		1	1		1		1	1	8
$e_5$	1	1	1		0			1					4
$e_6$				1		0		1		1	1		4
$e_7$	1		1	1			0		1	1			5
$e_8$		1			1	1		0			1		4
$e_9$			1	1			1		0	1	1		5
$e_{10}$	1		1			1	1		1	0	1		6
$e_{11}$	1			1		1		1	1	1	0	1	7
$e_{12}$				1							1	0	2

Перенумеруем вершины, чтобы получить второй граф (см. таблицу ниже)

V/V	$h_1$	$h_2$	$h_3$	$h_4$	$h_5$	$h_6$	$h_7$	$h_8$	$h_9$	$h_{10}$	$h_{11}$	$h_{12}$	p(h)
$h_1$	0	1							1				2
$h_2$	1	0	1	1	1		1		1			1	7
$h_3$		1	0	1		1	1			1		1	6
$h_4$		1	1	0		1			1	1			5
$h_5$		1			0		1	1			1		4
$h_6$			1	1		0			1	1		1	5
$h_7$		1	1		1		0		1				4
$h_8$					1			0		1	1	1	4
$h_9$	1	1		1		1	1		0	1	1	1	8
$h_{10}$			1	1		1		1	1	0	1	1	7
$h_{11}$					1			1	1	1	0		4
$h_{12}$		1	1			1		1	1	1		0	6

Для графа G1 ∑p(e)=62. Список P(e) = {8, 7, 7, 6, 6, 5, 5, 4, 4, 4, 4, 2} Для графа G2 ∑p(h)=62. Список P(h) = {8, 7, 7, 6, 6, 5, 5, 4, 4, 4, 4, 2}

	p(e)=p(h)=8	p(e)=p(h)=7	p(e)=p(h)=6	p(e)=p(h)=5	p(e)=p(h)=4	p(e)=p(h)=2
E	e4	e3,e11	e1,e10	e7,e9	e2,e5,e6,e8	e12
H	h9	h2,h10	h3,h12	h4,h6	h5,h7,h8,h11	h1

Из таблицы сразу видно соответствие вершин e4 – h9, e12-h1.
Попробуем установить соответствие между p(e) = p(h) = 6

Видим, что e1 – h12, e12 – h3

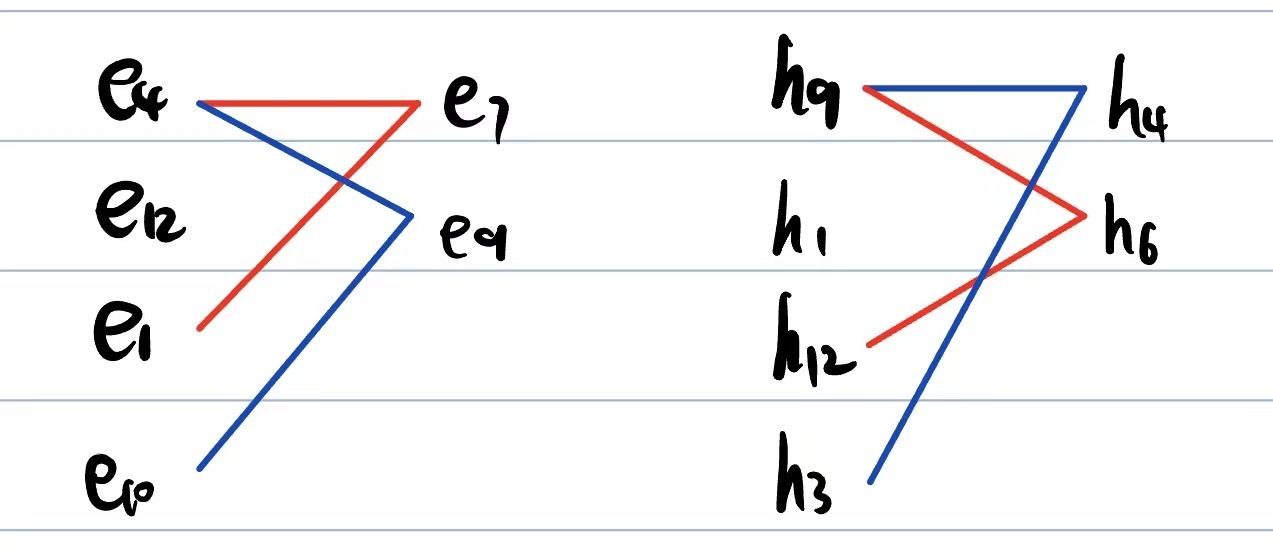
Видим, что e7 – h6, e9 – h4

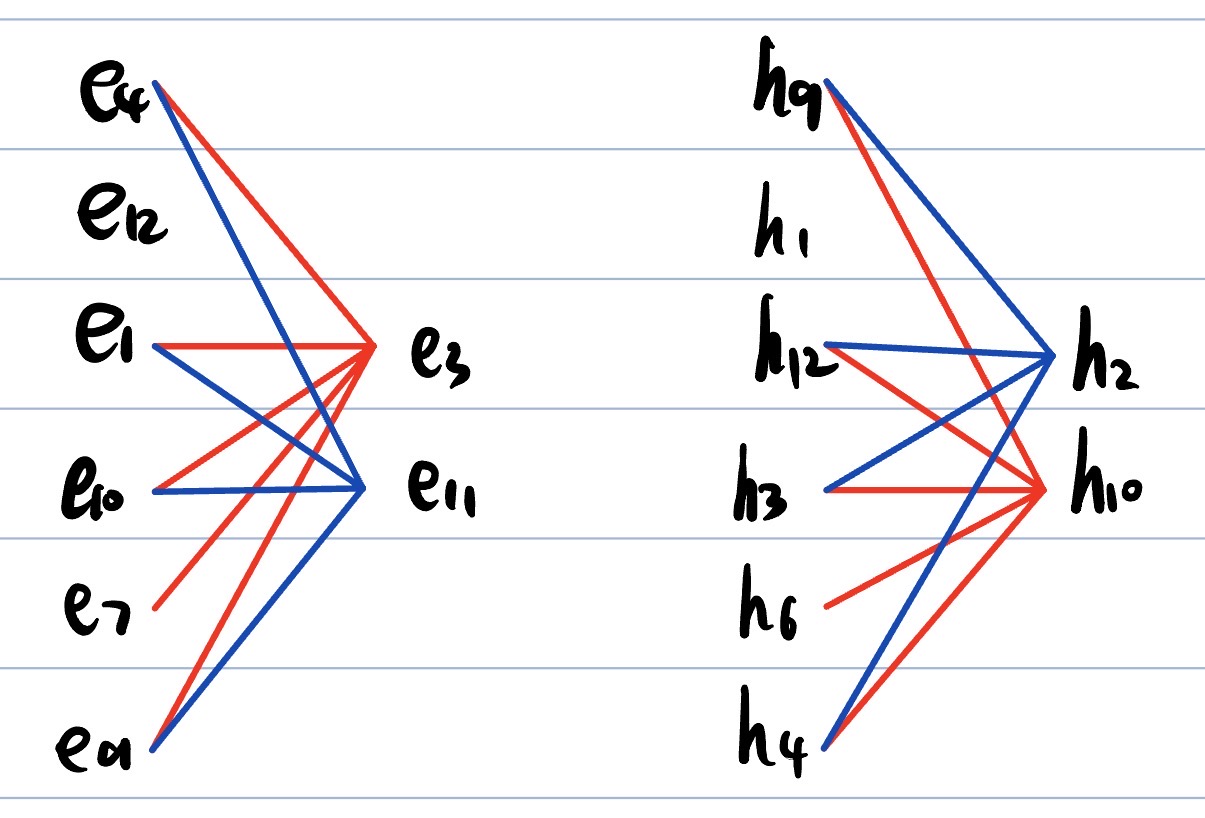
Видим, что e3 – h10, e11 – h2

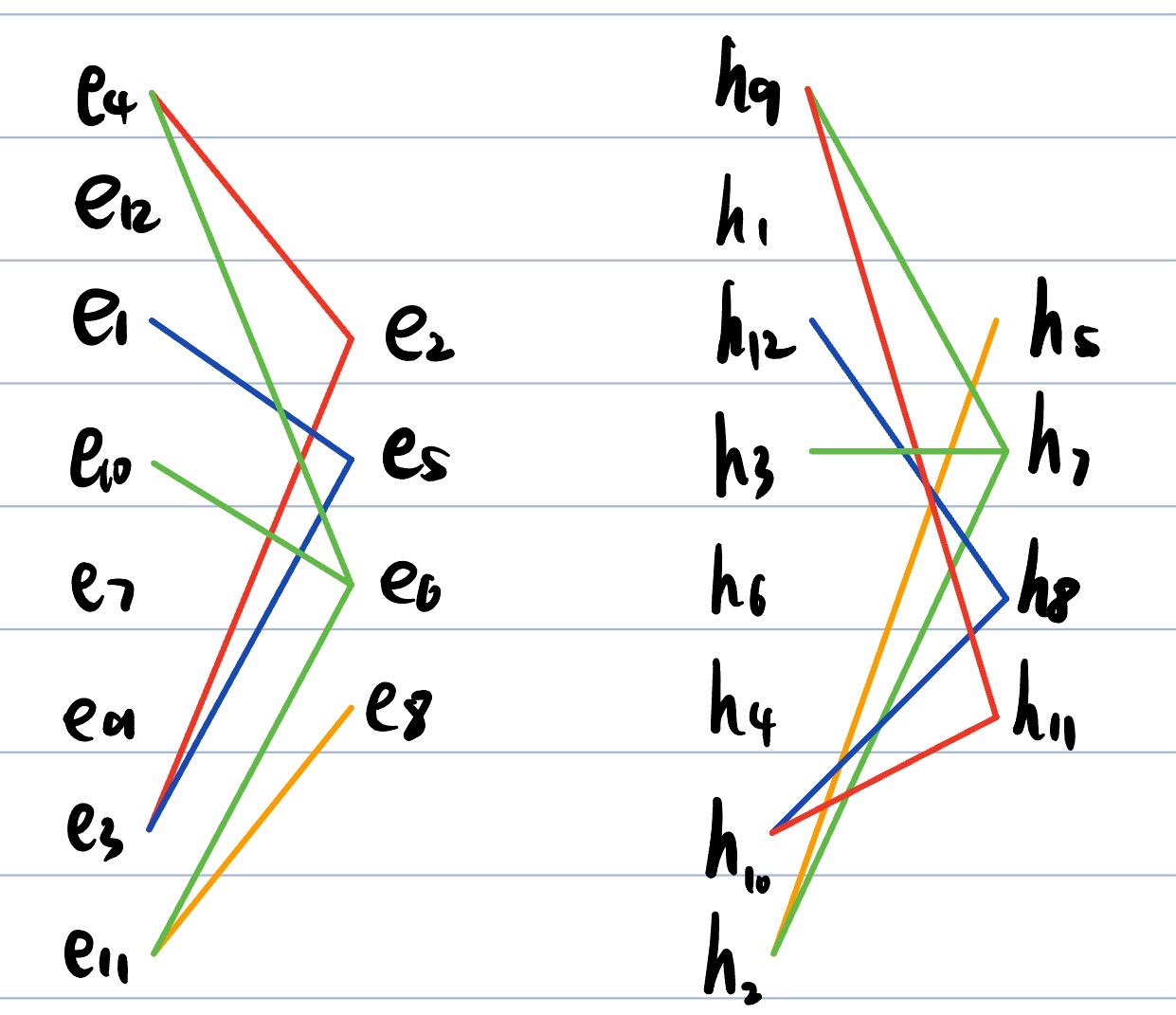
Видим, что e2 – h11, e5 – h8, e6 - h7, e8 - h5

Из всего этого заключаем, что наши графы изоморфны.