View on GitHub

ITMO-PE

My study notes about Program Engineering at University ITMO

MainPage/Mathematics/Типовой Расчёт

Типовой Расчёт 1

Задание №1

\[\begin{split} &\int\frac{e^{\tan{x}}+2}{\cos^2{x}}{\rm d}x\\ =&\int(e^{\tan{x}}+2)\sec^2{x}{\rm d}x\\ =&\int(2\sec^2(x)+e^{\tan{x}}\sec^2{x}){\rm d}x\\ =&\int e^{\tan{x}}\sec^2{x}{\rm d}x+2\int\sec^2(x){\rm d}x\\ &Пуcть\ u=\tan{x}\ и\ {\rm d}u=\sec^2{x}\\ =&\int e^u{\rm d}u+2\int\sec^2(x){\rm d}x\\ =&e^u+2\int\sec^2(x){\rm d}x+C\\ =&e^{\tan{x}}+2\tan(x)+C \end{split}\]

Задание №2

\[\begin{split} &\int\sin^2{(2x+1)}\cdot \cos^2{(2x+1)}{\rm d}x\\ &Пуcть\ u=2x+1\ и\ {\rm d}u=2{\rm d}x\\ =&\frac{1}{2}\int\sin^2(u)\cos^2(u){\rm du}\\ =&\frac{1}{2}\int\sin^2(u)(1-\sin^2(u)){\rm d}u\\ =&\frac{1}{2}\int(\sin^2(u)-\sin^4(u)){\rm d}u\\ =&\frac{1}{2}\int\sin^2(u){\rm d}u-\frac{1}{2}\int\sin^4(u){\rm}u\\ =&\frac{1}{8}\sin^3(u)\cos(u)+\frac{1}{8}\int\sin^2(u){\rm d}u\\ =&\frac{1}{8}\sin^3(u)\cos(u)+\frac{1}{8}\int\frac{1-\cos(2u)}{2}{\rm d}u\\ =&\frac{1}{8}\sin^3(u)\cos(u)-\frac{1}{16}\int\cos(2u){\rm d}u+\frac{1}{16}\int 1{\rm d}u\\ =&\frac{1}{8}\sin^3(u)\cos(u)-\frac{1}{32}\int\cos(2u){\rm d}(2u)+\frac{1}{16}\int 1{\rm d}u\\ =&-\frac{\sin(2u)}{32}+\frac{1}{8}\sin^3(u)\cos(u)+\frac{1}{16}\int 1{\rm d}u\\ =&-\frac{\sin(2u)}{32}+\frac{u}{16}+\frac{1}{8}\sin^3(u)\cos(u)+C\\ =&-\frac{\sin(4x+2)}{32}+\frac{2x+1}{16}+\frac{1}{8}\sin^3(2x+1)\cos^3(2x+1)+C \end{split}\]

Задание №3

\[\begin{split} &\int\frac{(2-x){\rm d}x}{\sqrt{3x^2+2x-5}}\\ &{\rm d}(3x^2+2x-5)=(6x+2){\rm d}x\\ =&-\frac{1}{6}\int\frac{6x+2}{\sqrt{3x^2+2x-5}}{\rm d}x+\frac{7}{3}\int\frac{ {\rm d}x}{\sqrt{3x^2+2x-5}}\\ &Пусть\ u=3x^2+2x-5, {\rm d}u=(6x+2){\rm d}x\\ =&-\frac{1}{6}\int\frac{ {\rm d}u}{\sqrt{u}}+\frac{3}{7}\int\frac{ {\rm d}x}{\sqrt{3x^2+2x-5}}\\ =&-\frac{1}{3}\sqrt{u}+\frac{3}{7}\int\frac{ {\rm d}x}{\sqrt{3x^2+2x-5}}+C\\ =&-\frac{1}{3}\sqrt{u}+\frac{3}{7}\int\frac{ {\rm d}x}{\sqrt{(\sqrt{3}x+\frac{1}{\sqrt{3}})^2-\frac{16}{3}}}+C\\ &Заменим\ впоследнем\ интеграле\ t=\sqrt{3}x+\frac{1}{\sqrt{3}}, k^2=\frac{16}{3}, {\rm d}x=\frac{1}{\sqrt{3}} {\rm d}t\\ =&-\frac{1}{3}\sqrt{u}+\frac{3}{7\sqrt{3}}\int\frac{ {\rm d}x}{\sqrt{t^2-k^2}}+C\\ =&-\frac{1}{3}\sqrt{u}+\frac{3}{7\sqrt{3}}\arcsin(\frac{k}{t})+C\\ =&-\frac{1}{3}\sqrt{u}+\frac{3}{7\sqrt{3}}\arcsin(\frac{k}{t})+C\\ =&-\frac{1}{3}\sqrt{3x^2+2x-5}+\frac{3}{7\sqrt{3}}\arcsin(\frac{\sqrt{\frac{16}{3}}}{\sqrt{3}x+\frac{1}{\sqrt{3}}})+C\\ =&-\frac{1}{3}\sqrt{3x^2+2x-5}+\frac{3\sqrt{3}}{21}\arcsin(\frac{\sqrt{16}}{3x+1})+C \end{split}\]

Задание №4

\[\begin{split} &\int\frac{x(x+4){\rm d}x}{(x+2)^2(x^2-3x+8)}\\ &Пусть \frac{x(x+4){\rm d}x}{(x+2)^2(x^2-3x+8)}=\frac{A}{x+2}+\frac{B}{(x+2)^2}+\frac{Cx+D}{x^2-3x+8}\\ &\begin{cases} 0=16A+8B+4D\\ 4=2A-3B+4C+4D\\ 1=-A+B+4C+D\\ 0=A+C \end{cases}\Rightarrow \begin{cases} A=-\frac{7}{81}\\ B=-\frac{2}{9}\\ C=\frac{7}{81}\\ D=\frac{64}{81} \end{cases}\\ =&\int\frac{7x+64}{81(x^2-3x+8)}-\frac{7}{81(x+2)}-\frac{2}{9(x+2)^2} {\rm d}x\\ =&\frac{1}{81}\int\frac{7x+64}{x^2-3x+8} {\rm d}x-\frac{7}{81}\int\frac{1}{x+2} {\rm d}x-\frac{2}{9}\int\frac{1}{(x+2)^2}{\rm d}x\\ =&\frac{1}{81}\int\frac{7x+64}{x^2-3x+8} {\rm d}x-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{7}{162}\int\frac{2x-3}{x^2-3x+8}{\rm d}x+\frac{149}{162}\int\frac{ {\rm d}x}{x^2-3x+8}-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ &Пусть\ u=x^2-3x+8,{\rm d}u=2x-3{\rm d}x\\ =&\frac{7}{162}\int\frac{ {\rm d}u}{u}+\frac{149}{162}\int\frac{ {\rm d}x}{x^2-3x+8}-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{149}{162}\int\frac{ {\rm d}x}{x^2-3x+8}+\frac{7}{162}\ln(u)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{149}{162}\int\frac{ {\rm d}x}{x^2-3x+8}+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{149}{162}\int\frac{ {\rm d}x}{(x-\frac{3}{2})^2+\frac{23}{4}}+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ &Пусть\ s=x-\frac{3}{2},{\rm d}s={\rm d}x\\ =&\frac{149}{162}\int\frac{ {\rm d}s}{(s)^2+\frac{23}{4}}+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{298}{1863}\int\frac{ {\rm d}s}{\frac{4s^2}{23}+1}+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ &Пусть\ v=\frac{2u}{\sqrt{23}},{\rm d}v=\frac{2}{\sqrt{23}}{\rm d}u\\ =&\frac{298}{1863}\frac{2}{\sqrt{23}}\int\frac{ {\rm d}v}{v^2+1}+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ =&\frac{298}{1863}\frac{2\sqrt{23}}{23}\arctan(s)+\frac{7}{162}\ln(x^2-3x+8)-\frac{7}{81}\ln(x+2)+\frac{2}{9(x+2)}+C\\ \end{split}\]

Задание №5

\[\begin{split} &\int\frac{ {\rm d}x}{2\sqrt{x+5}-\sqrt[3]{x+5}-\sqrt[4]{x+5}}\\ &Здесь\ k_1=3,k_2=2,поэтому\ p=12.\\ &Пусть\ x+5=t^{12}\ Тогда\ x=t^{12}-5,{\rm d}x=12t^{11}{\rm d}t\\ =&\int\frac{12t^{11} {\rm d}t}{2t^6-t^4-t^3}\\ =&12\int\frac{t^{11}{\rm d}t}{2t^6-t^4-t^3}\\ =&12\int\frac{t^8{\rm d}t}{2t^3-t-1}\\ &разделить\ \frac{t^8{\rm d}t}{2t^3-t-1}, получим:\\ &\frac{t^8{\rm d}t}{2t^3-t-1}=\frac{t^5}{2}+\frac{t^4}{4}+\frac{t^2}{4}+\frac{t}{8}+\frac{1}{5(t-1)}+\frac{-t-2}{40(2t^2+2t+1)}+\frac{1}{4}\\ =&12\int\frac{t^5}{2}+\frac{t^4}{4}+\frac{t^2}{4}+\frac{t}{8}+\frac{1}{5(t-1)}+\frac{-t-2}{40(2t^2+2t+1)}+\frac{1}{4}{\rm d}t\\ =&\frac{3}{10}\int\frac{-t-2}{2t^2+t+1}{\rm d}t+6\int t^5{\rm d}t+3\int t^3{\rm d}t+3\int t^2{\rm d}t+\frac{3}{2}\int t{\rm d}t+\frac{12}{5}\int\frac{ {\rm d}t}{t-1}+3\int {\rm d}t\\ =&\frac{3}{10}\int\left(-\frac{4t+2}{4(2t^2+2t+1)}-\frac{3}{2(2t^2+2t+1)}\right){\rm d}t+6\int t^5{\rm d}t+3\int t^3{\rm d}t+3\int t^2{\rm d}t+\frac{3}{2}\int t{\rm d}t+\frac{12}{5}\int\frac{ {\rm d}t}{t-1}+3\int {\rm d}t\\ =&-\frac{3}{40}\int\frac{4t+2}{2t^2+2t+1}{\rm d}t-\frac{9}{20}\int\frac{ {\rm d}t}{2t^2+2t+1}+6\int t^5{\rm d}t+3\int t^3{\rm d}t+3\int t^2{\rm d}t+\frac{3}{2}\int t{\rm d}t+\frac{12}{5}\int\frac{ {\rm d}t}{t-1}+3\int {\rm d}t\\ =&-\frac{3}{40}\int\frac{ {\rm d}(2t^2+2t+1)}{2t^2+2t+1}-\frac{9}{20}\int\frac{ {\rm d}t}{(\sqrt{2}t+\frac{1}{\sqrt{2}})^2+\frac{1}{2}}+6\int t^5{\rm d}t+3\int t^3{\rm d}t+3\int t^2{\rm d}t+\frac{3}{2}\int t{\rm d}t+\frac{12}{5}\int\frac{ {\rm d}t}{t-1}+3\int {\rm d}t\\ =&-\frac{3}{40}\int\frac{ {\rm d}(2t^2+2t+1)}{2t^2+2t+1}-\frac{9}{10\sqrt{2}}\int\frac{ {\rm d}(\sqrt{2t}+\frac{1}{\sqrt{2}})}{2(\sqrt{2}t+\frac{1}{\sqrt{2}})^2+1}+6\int t^5{\rm d}t+3\int t^3{\rm d}t+3\int t^2{\rm d}t+\frac{3}{2}\int t{\rm d}t+\frac{12}{5}\int\frac{ {\rm d}t}{t-1}+3\int {\rm d}t\\ =&-\frac{3}{40}\ln(2t^2+2t+1)-\frac{9}{20}\arctan(2t+1)+t^6+\frac{3}{4}t^4+t^3+\frac{3}{4}t^2+\frac{12}{5}\ln(t-1)+3t+C\\ &(t=\sqrt[12]{x+5}) \end{split}\]

Задание №6

\[\begin{split} &\int\frac{\sqrt{(1-x^2)^3}}{x^2}{\rm d}x\\ =&\int\frac{(1-x^2)\sqrt{1-x^2}}{x^2}{\rm d}x\\ =&\int\frac{\sqrt{1-x^2}}{x^2}{\rm d}x-\int\sqrt{1-x^2}{\rm d}x\\ &a=1,x=a\sin t=\sin t,{\rm d}x=\cos t{\rm d}t\\ =&\int\frac{\sqrt{1-\cos^2t}}{\sin^2t}\cos t{\rm d}t-\int\sqrt{1-\sin^2t}\cos t{\rm d}t\\ =&\int\frac{\cos t}{\sin t}{\rm d}t-\int\cos^2t{\rm d}t\\ =&\int\frac{ {\rm d}(\sin t)}{\sin t}-\frac{1}{2}\int(\cos(2t)+1){\rm d}t\\ =&\ln(\sin t)-\frac{1}{4}\int\cos(2t){\rm d}(2t)-\frac{1}{2}\int{\rm d}t+C\\ =&\ln(\sin t)-\frac{1}{4}\sin(2t)-\frac{t}{2}+C\\ &t=\arcsin x\\ =&\ln x-\frac{1}{2}(x\sqrt{1-x^2})-\frac{1}{2}\arcsin x+C \end{split}\]

Задание №7

\[\begin{split} &\int\frac{\cos{x}{\rm d}x}{(1-\cos{x})^3}\\ &Пусть\ t=\tan\frac{x}{2},то\ x=2\arctan t,{\rm d}x=\frac{2{\rm d}t}{1+t^2}\\ &\sin x=2\frac{\tan\frac{x}{2}}{1+\tan^2\frac{x}{2}}=\frac{2t}{1+t^2};\cos x=\frac{1-\tan^2\frac{x}{2}}{1+\tan^2\frac{x}{2}}=\frac{1-t^2}{1+t^2}\\ =&\int\frac{2(1-t^2)}{(1+t^2)^2(1-\frac{1-t^2}{1+t^2})^3}{\rm d}t\\ =&\int\frac{1-t^4}{4t^6}{\rm d}t\\ =&\frac{1}{4}\int\frac{1-t^4}{t^6}{\rm d}t\\ =&\frac{1}{4}\int\frac{1}{t^6}{\rm d}t-\frac{1}{4}\int\frac{1}{t^2}{\rm d}t\\ =&\frac{1}{4t}-\frac{1}{20t^5}+C\\ &t=\tan\frac{x}{2}\\ =&\frac{1}{4}\cot\frac{x}{2}-\frac{1}{20}\cot^5\frac{x}{2}+C \end{split}\]

Задание №8

\[\begin{split} &\int^\frac{2}{3}_\frac{1}{3}(x^2-x+1)e^{3x}{\rm d}x\\ =&\int^\frac{2}{3}_\frac{1}{3}(e^{3x}x^2-e^{3x}x+e^{3x}){\rm d}x\\ =&\int^\frac{2}{3}_\frac{1}{3}e^{3x}x^2{\rm d}x-\int^\frac{2}{3}_\frac{1}{3}e^{3x}e{\rm d}x+\int^\frac{2}{3}_\frac{1}{3}e^{3x}{\rm d}x\\ &u=x^2,{\rm d}u=2x{\rm d}x\\ &{\rm d}v=e^{3x},v=\frac{e^{3x}}{3}\\ =&\left.\frac{1}{3}e^{3x}x^2\right|^\frac{2}{3}_\frac{1}{3}-\frac{5}{3}\int^\frac{2}{3}_\frac{1}{3}e^{3x}x{\rm d}x+\int^\frac{2}{3}_\frac{1}{3}e^{3x}{\rm d}x\\ =&\frac{1}{27}e(4e-1)-\frac{5}{3}\int^\frac{2}{3}_\frac{1}{3}e^{3x}x{\rm d}x+\int^\frac{2}{3}_\frac{1}{3}e^{3x}{\rm d}x\\ &u'=x,{\rm d}u'={|rm d}x\\ &{\rm d}v'=e^{3x},v'=\frac{e^{3x}}{3}\\ =&\frac{1}{27}e(4e-1)+\left.(-\frac{5}{9}e^{3x})\right|^\frac{2}{3}_\frac{1}{3}+\frac{14}{9}\int^\frac{2}{3}_\frac{1}{3}e^{3x}{\rm d}x\\ =&\frac{1}{27}e(4e-1)-\frac{5}{27}e(2e-1)+\frac{14}{9}e^{3x}{\rm d}x\\ =&\frac{1}{27}e(4e-1)-\frac{5}{27}e(2e-1)+\left.\frac{14}{27}e^{3x}\right|^\frac{2}{3}_\frac{1}{3}\\ =&\frac{1}{27}e(4e-1)-\frac{5}{27}e(2e-1)+\frac{14}{27}e(e-1)\\ =&\frac{2}{27}e(4e-5) \end{split}\]

Задание №9

\[\begin{split} &\int^\frac{\pi}{2}_0\sin{\varphi}\sqrt{\cos{\varphi}}{\rm d}\varphi\\ &Пусть\ \phi=\cos\varphi,{\rm d}\phi={\rm d}\varphi\\ =&-\int^0_1\sqrt{\phi}{\rm d}\phi\\ =&\int^1_0\sqrt{\phi}{\rm d}\phi\\ =&\left.\frac{2}{3}\phi^\frac{3}{2}\right|^1_0\\ =&\frac{2}{3} \end{split}\]

Задание №10

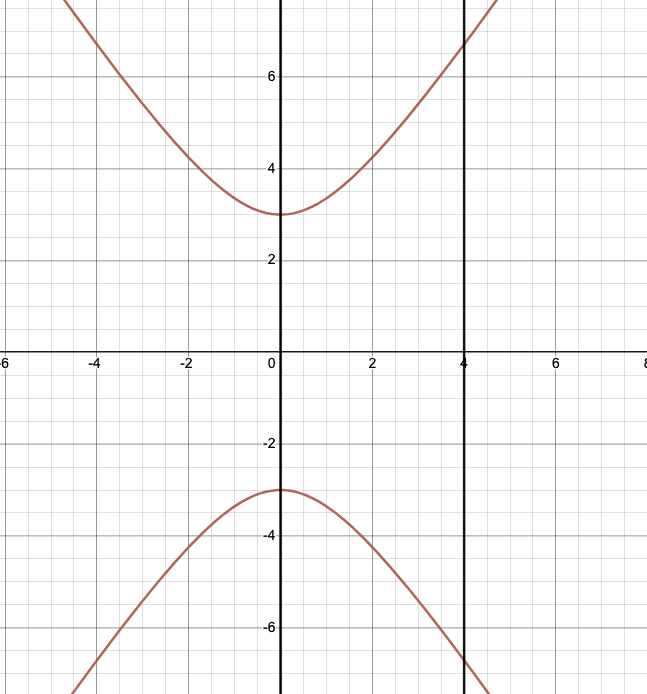
Найдите площадь области, ограниченной кривыми, заданными в декартовых координатах

График Функция
\[\begin{cases} f_1:x^2+y^2=16x\\ f_2:y^2=8x\\ \end{cases}\Rightarrow \begin{cases} f_1:y=\sqrt{16x-x^2}\\ f_2:y=2\sqrt{2x} \end{cases}\]

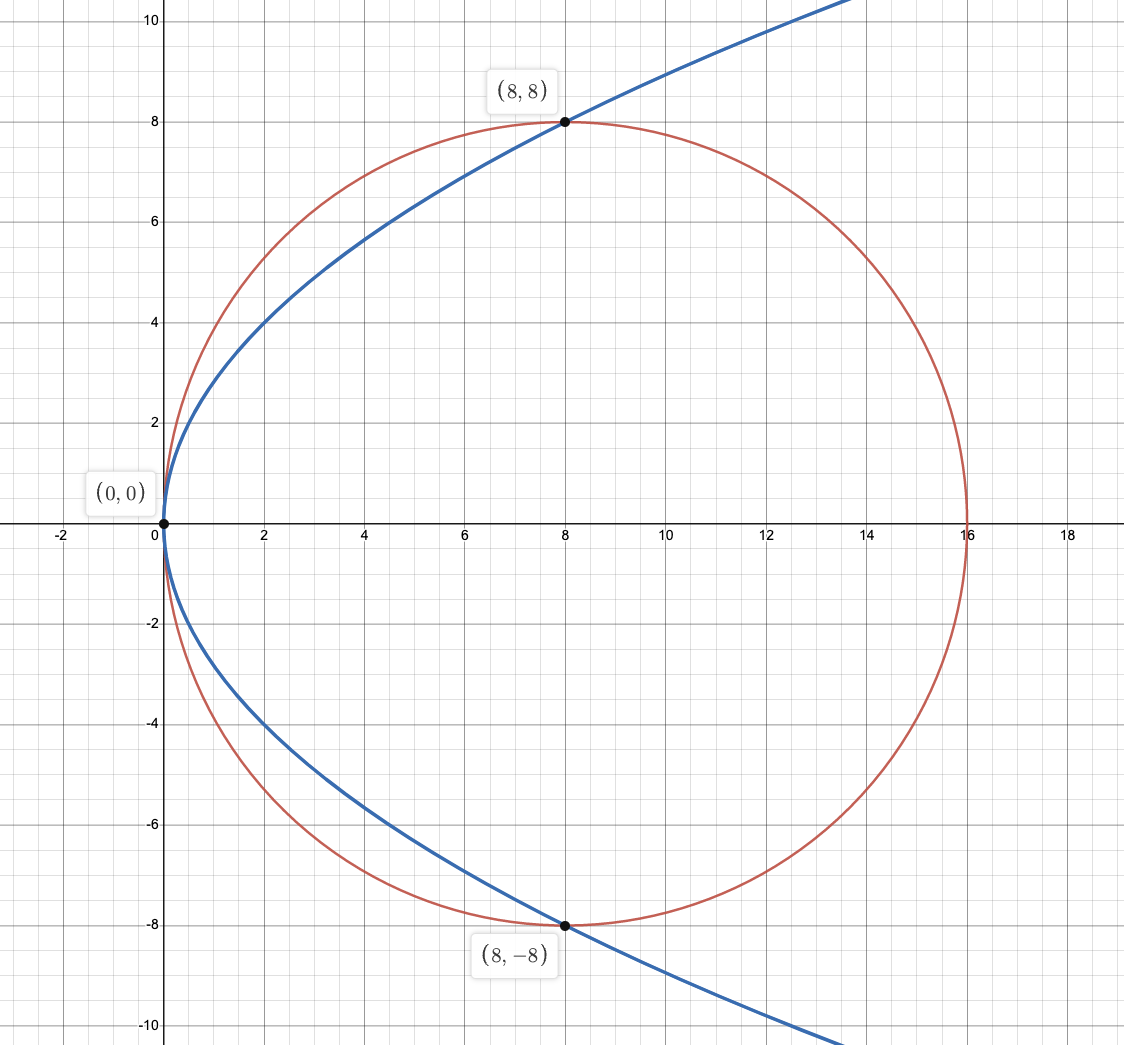
Очевидно, что $f_1$ - окружность,и Площать $S_1=64\pi$

\[\begin{split} &Пусть\ S_\Delta=\int^8_0(f_1-f_2){\rm d}x=\int^8_0(\sqrt{16x-x^2}-2\sqrt{2x}){\rm d}x\\ &=16\pi-\int^8_02\sqrt{2x}{\rm d}x\\ &=16\pi-2\sqrt{2}\int^8_0\sqrt{x}{\rm d}x\\ &=16\pi-\left.\frac{4}{3}\sqrt{2}x^\frac{3}{2}\right|^8_0\\ &=16\pi-\frac{128}{3}\\ & \end{split}\]

Площадь области,ограниченной заданными кривыми $S$:

\[S=S_1-2S\Delta=64\pi-2(16\pi-\frac{128}{3})=32\pi+\frac{256}{3}\]

Задание №11

Найдите длину кривой $L$, заданной в декартовых координатах

\[y^2-2y=4x\quad -1\le x\le 0\]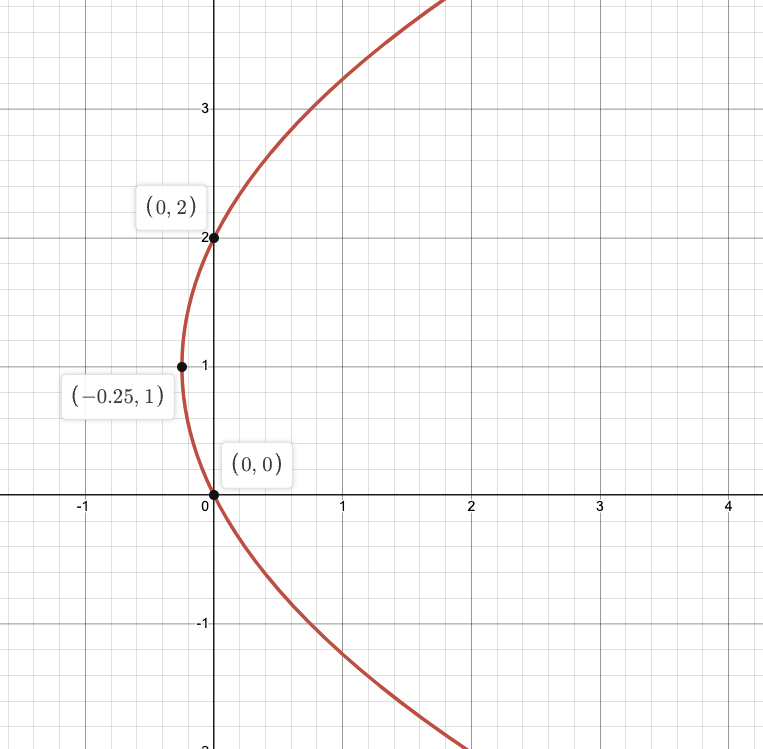
График Функция

Очевидно, что L равна его обратной фукцией в части $(-1\le y\le 0)$:

\[x^2-2x=4y\quad -1\le y\le 0\]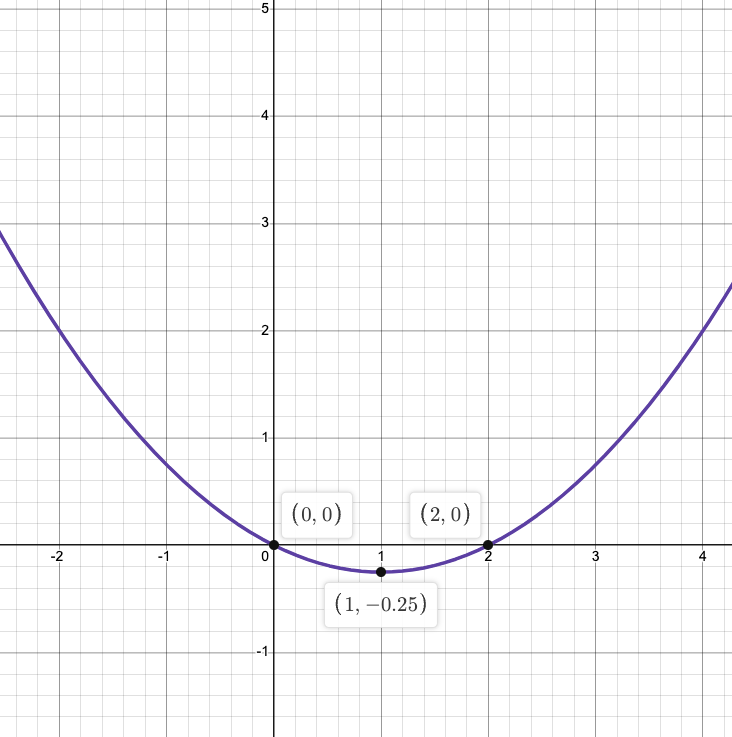
График Функция
\[\begin{split} x^2&-2x=4y\\ \Rightarrow y&=\frac{x^2}{4}-\frac{x}{2}\\ y'&=\frac{x}{2}-\frac{1}{2}\\ L&=\int^0_{-1}\sqrt{1+y'^2}{\rm d}x\\ &=\int^0_{-1}\sqrt{1+(\frac{x}{2}-\frac{1}{2})^2}{\rm d}x\\ &=\frac{1}{2}\int^0_{-1}\sqrt{x^2-2x+5}{\rm d}x\\ Пусть\ u&=x-1,{\rm d}u={\rm d}x\\ L&=\frac{1}{2}\int^{-1}_{-2}\sqrt{u^2+4}{\rm d}u\\ Пусть\ u&=2\tan(t),{\rm d}u=2\sec^2(t){\rm d}t\\ L&=2\int^{-\arctan\frac{1}{2}}_{-\frac{\pi}{4}}\sec^3(t){\rm d}t\\ &=\left.\tan(t)\sec(t)\right|^{-\arctan\frac{1}{2}}_{-\frac{\pi}{4}}+\int^{-\arctan\frac{1}{2}}_{-\frac{\pi}{4}}\sec(t){\rm d}t\\ &=\sqrt{2}-\frac{\sqrt{5}}{4}+\int^{-\arctan\frac{1}{2}}_{-\frac{\pi}{4}}\sec(t){\rm d}t\\ &=\sqrt{2}-\frac{\sqrt{5}}{4}+\left.\ln(\tan(t)+\sec(t))\right|^{-\arctan\frac{1}{2}}_{-\frac{\pi}{4}}\\ &=\sqrt{2}-\frac{\sqrt{5}}{4}-\ln(\sqrt{2}-1)+\ln(\frac{1}{2}(\sqrt{5}-1)) \end{split}\]

Задание №12

Вычислите

\[\begin{cases} x=2t\\ y=\frac{8}{1+t^2} \end{cases}\]

Из формулы $x$ получим $t=\frac{x}{2}$, подставляем в $y$:

\[\begin{split} y&=\frac{8}{1+(\frac{x}{2})^2}=\frac{32}{x^2+4}\\ S&=\int^{+\infty}_{-\infty}\frac{32}{x^2+4}{\rm d}x\\ &=32\int^{+\infty}_{\infty}\frac{1}{x^2+4}{\rm d}x\\ &=64\int^{\infty}_0\frac{1}{x^2+4}{\rm d}x\\ &=32\int^{\infty}_0\frac{1}{\frac{x^2}{4}+1}{\rm d}(\frac{x}{2})\\ &=\left.\lim_{a\rightarrow\infty}32\arctan(\frac{x}{2})\right|^a_0\\ &=16\pi \end{split}\]

Задание №13

Найдите значение несобственного интеграла или установите его расходимость.

\[\begin{split} &\int^{+\infty}_0(4-3x)e^{-3x}{\rm d}x\\ =&4\int^{+\infty}_0e^{-3x}{\rm d}x-3\int^{+\infty}_0xe^{-3x}{\rm d}x\\ =&4\lim_{b\rightarrow\infty}\int^{b}_0e^{-3x}{\rm d}x-3\lim_{b\rightarrow\infty}\int^{b}_0xe^{-3x}{\rm d}x\\ =&3\lim_{b\rightarrow\infty}\int^b_0e^{-3x}{\rm d}x+\left.\lim_{b\rightarrow\infty}xe^{-3x}\right|^b_0\\ =&3\lim_{b\rightarrow\infty}\int^b_0e^{-3x}{\rm d}x+\lim_{b\rightarrow\infty}be^{-3b}\\ =&3\lim_{b\rightarrow\infty}\int^b_0e^{-3x}{\rm d}x+0\\ =&\left.e^{-3b}\right|^{0}_{-\infty}\\ =&1 \end{split}\] \[\begin{split} &\int^\frac{1}{2}_0\frac{x^3{\rm d}x}{\sqrt{1-16x^4}}\\ Пусть\ u=&1-16x^4\quad{\rm d}u=-64x^3{\rm d}x\\ =&-\frac{1}{64}\int^0_1\frac{1}{\sqrt{u}}{\rm d}u\\ =&\frac{1}{64}\int^1_0\frac{1}{\sqrt{u}}{\rm d}u\\ =&\left.\lim_{b\rightarrow0^+}\frac{\sqrt u}{32}\right|^1_b\\ =&\frac{\sqrt{1}}{32}-\frac{\sqrt{0}}{32}\\ =&\frac{1}{32} \end{split}\]

Типовой Расчёт 2

Задание №1

Найдите область определения функций:

\[z=\lg(x-2)(y-1)+\frac{y}{x+1}\] \[\begin{split} \begin{cases} (x-2)(y-1)>0\\ x+1\ne0 \end{cases} \end{split}\]
График Функция
\[z=\ln(x^2+y^2-16)+\frac{1}{\sqrt{4-x^2-y^2}}\] \[\begin{cases} x^2+y^2-16>0\\ 4-x^2-y^2>0 \end{cases}\]
График Функция

Задание №2

Найдите частные производные первого порядка функции

\[z=\frac{5x+y\cdot\tan x}{\sqrt{x^2+y^2}}\] \[\begin{split} z'_x&=\frac{\partial}{\partial x}(\frac{5x+y\cdot\tan x}{\sqrt{x^2+y^2}})\\ Пусть&\begin{cases} u=5x+y\cdot\tan(x)\\ v=\frac{1}{\sqrt{x^2+y^2}} \end{cases} \\ \frac{\partial}{\partial x}&(uv)=\frac{\partial u}{\partial x}v+\frac{\partial v}{\partial x}u\\ z'_x&=\frac{\frac{\partial}{\partial x}(5x+y\cdot\tan(x))}{\sqrt{x^2+y^2}}+(\frac{\partial}{\partial x}\frac{1}{\sqrt{x^2+y^2}})(5x+y\tan(x))\\ &=\frac{5+y\cdot\sec^2(x)}{\sqrt{x^2+y^2}}-\frac{x(5x+y\tan(x))}{\sqrt{(x^2+y^2)^3}}\\ z'_y&=\frac{\partial}{\partial y}(\frac{5x+y\cdot\tan(x)}{\sqrt{x^2+y^2}})\\ \frac{\partial}{\partial y}&(uv)=\frac{\partial u}{\partial y}v+\frac{\partial v}{\partial y}u\\ z'_y&=\frac{\frac{\partial}{\partial y}(5x+y\cdot\tan(x))}{\sqrt{x^2+y^2}}+(\frac{\partial}{\partial y}\frac{1}{\sqrt{x^2+y^2}})(5x+y\tan(x))\\ &=\frac{\tan(x)}{\sqrt{x^2+y^2}}-\frac{y(5x+y\tan(x))}{\sqrt{(x^2+y^2)^3}} \end{split}\]

Задание №3

Найдите частные производные функции $z=z(x;y)$, заданной неявной уравнением $8x^3-3y^2+z^2-\sin z+2x-3y+1=0$

\[F'_x(x,y,z)=24x^2+2, F'_y(x,y,z)=6y-3,F'_z(x,y,z)=2z-\cos z\] \[z'_x=-\frac{F'_x(x,y,z)}{F'_z(x,y,z)}=\frac{24x^2+2}{2z-\cos z}\] \[z'_y=-\frac{F'_y(x,y,z)}{F'_z(x,y,z)}=\frac{6y-3}{2z-\cos z}\]

Задание №4

Найдите градиент функции $z=2x^4-3y^3+x+2y$ в точке $M_0(2;1)$ и производную по направлению вектора $\vec{M_0M_1}$, где $M_1(5;3)$

\[\begin{split} z'_x&=\frac{\partial}{\partial x}(2x^4-3y^3+x+2y)=8x^3+1 \\ z'_x&(2;1)=65\\ z'_y&=\frac{\partial}{\partial y}(2x^4-3y^3+x+2y)=-9y^2+2 \\ z'_y&(2;1)=-7\\ \end{split}\]

тогда $\nabla z={65;-7}$

\[\begin{split} z'_l(x;y)&=z'_x\cdot\cos\alpha+z'_y\cdot\cos\beta\\ \vec{M_0M_1}&=(5-2;3-1)=(3;2)\\ |\vec{M_0M_1}|&=\sqrt{x^2+y^2}=\sqrt{13}\\ \cos\alpha&=\frac{3}{\sqrt{13}},\cos\beta=\frac{2}{\sqrt{13}}\\ z'_l&=z'_x(3;2)\cos\alpha+z'_y(3;2)\cos\beta\\ &=65\times\frac{3}{\sqrt{13}}-7\frac{2}{\sqrt{13}}\\ &=\frac{195}{\sqrt{13}}-\frac{14}{\sqrt{13}} \end{split}\]

Задание №5

Составьте уравнения касательной плоскости и нормали к поверхкости $x^2+2y^2+z^2+4xz=6$ в точке $M_0(1;2;-1)$

\[F(x,y,z)=x^2+2y^2+z^2+4xz-6=0\] \[F'_x(x,y,z)=2x+4z,F'_y(x,y,z)=4y,F'_z(x,y,z)=2z+4x\]

уравнение касательной плоскости:

\[F'_x(M_0)(x-x_0)+F'_y(M_0)(y-y_0)+F'_z(M_0)(z-z_0)=0\] \[-2(x-1)+8(y-2)+2(z+1)=0\]

уравнение нормали:

\[\frac{x-x_0}{F'_x(M_0)}=\frac{y-y_0}{F'_y(M_0)}=\frac{z-z_0}{F'_z(M_0)}\] \[\frac{x-1}{-2}=\frac{y-2}{8}=\frac{z+1}{2}\]

Задание №6

Исследуйте на экстремуи функцию $z=x^3+3x^2-2y^2+10y-3$

\[\begin{split} z&=f(x;y)=x^3+3x^2-2y^2+10y-3\\ &\begin{cases} z'_x&=3x^2+6x\\ z'_y&=-4y+10\\ \end{cases}\\ &\begin{cases} z'_x=0\\ z'_y=0\\ \end{cases}\Rightarrow \begin{cases} 3x^2+6x=0\\ -4y+10=0\\ \end{cases}\\ \Rightarrow &\begin{cases} x=0,\\ y=\frac{5}{2}\\ \end{cases}, \begin{cases} x=-2\\ y=\frac{5}{2}\\ \end{cases}\\ &M_0(0,\frac{5}{2}),M_1(-2,\frac{5}{2})\\ &\begin{cases} z''_{xx}&=6x+6\\ z''_{yy}&=-4\\ z''_{xy}&=0\\ \end{cases}\\ &\begin{cases} z''_{xx}(M_0)=6\\ z''_{yy}(M_0)=-4\\ z''_{xy}(M_0)=0\\ \end{cases} \begin{cases} z''_{xx}(M_1)=-6\\ z''_{yy}(M_1)=-4\\ z''_{xy}(M_1)=0\\ \end{cases}\\ &\Delta(M_0)=\begin{vmatrix} 6 & 0\\ 0 & -4\\ \end{vmatrix}=-24-0=-24<0\\ &Следовательно,\ в\ стационарной точке\ M_0(0,\frac{5}{2})\ экстркмума\ нет\\ &\Delta(M_1)=\begin{vmatrix} -6 & 0\\ 0 & -4\\ \end{vmatrix}=24-0=24>0\\ &Следовательно,\ в\ стационарной точке\ M_1(-2,\frac{5}{2})\ экстркмум\ есть\\ &Так\ как\ z'_{xx}(M_1)=-6<0,\ то\ точка\ M_1(-2,\frac{5}{2})\ -\ точка\ максимума\\ &z_{\max}(-2,\frac{5}{2})=13.5 \end{split}\]
<img src="pic/TypeWork-6.png"width="800">
График Функция

Задание №7

Найдите наибольшее и наименьшее значение функции $z=f(x;y)$ в замкнутой области $D$, ограниченной заданными линиями

\[z=7-x^2-xy-y^2+3x-3y\] \[x=0;x=4;y=1;y=-4\] \[\begin{split} \begin{cases} z'_x=-2x-y+3=0\\ z'_y=-x-2y-3=0\\ \end{cases}\Rightarrow \begin{cases} x=3\\ y=-3\\ \end{cases}\\ (3;-3)\ лежит\ в\ D\\ z(3;-3)=7 \end{split}\]
График Функция
\[\begin{split} &Расмотрим\ AB\\ y&=1, 0\le x\le 4\\ z&=3-x^2+2x\\ z&(0;1)=3\\ z&(4;1)=-5\\ z'_x&=-2x+2\\ x&=1\\ &(1,1)\ лежит\ в\ AB\\ z&(1,1)=4 \end{split}\] \[\begin{split} &Расмотрим\ CD\\ y&=-4, 0\le x\le 4\\ z&=3-x^2+7x\\ z&(0;-4)=3\\ z&(4;-4)=15\\ z'_x&=-2x+7\\ x&=\frac{7}{2}\\ &(\frac{7}{2},-4)\ лежит\ в\ CD\\ z&(\frac{7}{2},-4)=15.25 \end{split}\] \[\begin{split} &Расмотрим\ AC\\ x&=0, -4\le y\le 1\\ z&=7-y^2-3y\\ z&(0;-4)=3\\ z&(0;1)=3\\ z'_y&=-2y-3\\ y&=-\frac{3}{2}\\ &(0,-\frac{3}{2})\ лежит\ в\ AC\\ z&(0,-\frac{3}{2})=9.25 \end{split}\] \[\begin{split} &Расмотрим\ BD\\ x&=4, -4\le y\le 1\\ z&=7-y^2-7y\\ z&(4;-4)=19\\ z&(4;1)=-1\\ z'_y&=-2y-7\\ y&=-\frac{7}{2}\\ &(0,-\frac{7}{2})\ лежит\ в\ BD\\ z&(0,-\frac{7}{2})=19,25 \end{split}\]

Сравниавя все найденные значения функции $z(3;-3),z(0;1),z(4;1),z(0;-4),z(0;-4),z(4;-4),z(1;1),z(\frac{7}{2},-4),z(0,-\frac{3}{2}),z(0,-\frac{7}{2})$ Получми $z_{\min}=z(1,1)=4,z_{\max}=z(0;-\frac{7}{2})=19.25$

Дополнительные задачи

Задание 1

a)

\[\begin{split} &\int^1_0\frac{2\arctan x+x}{1+x^2}{\rm d}x\\ =&2\int^1_0\frac{\arctan x}{x^2+1}+\int^1_0\frac{x}{x^2+1}\\ &Пусть\ u=\arctan x,{\rm d}u=\frac{1}{x^2+1}{\rm d}x\\ =&2\int^{\frac{\pi}{4}}_0u{\rm d}u+\int^1_0\frac{x}{x^2+1}{\rm d}x\\ =&\left.u^2\right|^{\frac{\pi}{4}}_0+\int^1_0\frac{x}{x^2+1}{\rm d}x\\ =&\frac{\pi^2}{16}+\int^1_0\frac{x}{x^2+1}{\rm d}x\\ &Пусть\ v=x^2=1,{\rm d}v=2x{\rm d}x\\ =&\frac{\pi^2}{16}+\frac{1}{2}\int^2_1\frac{1}{v}{\rm d}v\\ =&\frac{\pi^2}{16}+\left.\frac{\ln v}{2}\right|^2_1\\ =&\frac{\pi^2}{16}+\frac{\ln 2}{2} \end{split}\]

b)

\[\begin{split} &\int^{\frac{\pi}{4}}_0\frac{\sin x-\cos x}{(\cos x+\sin x)^3}{\rm d}x\\ &Пусть\ u=\sin x+\cos x,{\rm d}u=(\cos x-\sin x){\rm d}x\\ =&-\int^{\sqrt{2}}_1\frac{1}{u^3}{\rm d}u\\ =&\left.\frac{1}{2u^2}\right|^{\sqrt{2}}_1\\ =&\frac{1}{2\times2}-\frac{1}{2\times1}=-\frac{1}{4} \end{split}\]

c)

\[\begin{split} &\int^{e^{\frac{\pi}{2}}}_1\cos(\ln x){\rm d}x\\ &Пусть\ u=\ln x,{\rm d}u=\frac{1}{x}{\rm d}x\\ =&\int^{\frac{\pi}{2}}_0e^u\cos(u){\rm d}u\\ &Пусть\ f=\cos(u),{\rm d}f=-\sin(u){\rm d}u\\ &Пусть\ {\rm d}g=e^u{\rm d}u,g=e^u\\ &\int e^u\cos(u){\rm d}u\\ =&e^u\cos(u)+\int e^u\sin(u){\rm d}u\\ &Пусть\ f'=\sin(u),{\rm d}f'=\cos(u){\rm d}u\\ &Пусть\ {\rm d}g'=e^u{\rm d}u,g'=e^u\\ &\int e^u\cos(u){\rm d}u=e^u\sin(u)+e^u\cos(u)-\int e^u\cos(u){\rm d}u\\ &e^u\cos(u)=\frac{1}{2}(e^u\sin(u)+e^u\cos(u))\\ &\int^{\frac{\pi}{2}}_0e^u\cos(u){\rm d}u\\ =&\left.\frac{1}{2}(e^u\sin(u)+e^u\cos(u))\right|^{\frac{\pi}{2}}_0\\ =&\frac{1}{2}(e^{\frac{\pi}{2}}-1) \end{split}\]

Задание 2

a)

\[\begin{split} &\int^{+\infty}_0e^{-\sqrt{x}}{\rm d}x\\ &Пустт\ u=\sqrt{x},{\rm d}u=\frac{1}{2\sqrt{x}}{\rm d}x\\ =&2\int^{+\infty}_0e^{-u}u{\rm d}u\\ &Пусть\ f=u,{\rm d}f={\rm d}u\\ &Пусть\ {\rm d}g=e^{-u}{\rm d}u,g=e^{-u}\\ =&\lim_{a\rightarrow\infty}\left.(-2e^{-u}u)\right|^a_0+2\int^\infty_0e^{-u}{\rm d}u\\ =&\lim_{a\rightarrow\infty}-2e^{-a}a+2\int^\infty_0e^{-u}{\rm d}u\\ =&0+2\int^\infty_0e^{-u}{\rm d}u\\ &Пусть\ v=-u,{\rm d}v=-{\rm d}u\\ =&-2\int^{-\infty}_0e^v{\rm d}v\\ =&2\int^0_{-\infty}e^v{\rm d}v\\ =&\left.2e^v\right|^0_{-\infty}\\ =2 \end{split}\]

b)

\[\begin{split} &\int^1_0x^2\ln x{\rm d}x\\ &Пучть\ u=\ln x,{\rm d}u=\frac{1}{x}{\rm d}x\\ &Пучть\ {\rm d}v=x^2,v=\frac{x^3}{3}\\ =&\lim_{a\rightarrow0^+}\left.\frac{x^3}{3}\ln x\right|^1_a-\frac{1}{3}\int^1_0x^2{\rm d}x\\ =&-\frac{1}{3}\int^1_0x^2{\rm d}x\\ =&\left.-\frac{x^3}{9}\right|^1_0\\ =&-\frac{1}{9} \end{split}\]

Задание 3

a)

\[\begin{split} y_1&=\frac{8}{4+x^2}\\ y_2&=\frac{x^2}{4}\\ Пусть\ f(x)&=y_1-y_2=\frac{8}{4+x^2}-\frac{x^2}{4}=0\\ Получим\ x_1&=-2,x_2=2\\ S&=\int^2_{-2}f(x)=\int^2_{-2}(\frac{8}{4+x^2}-\frac{x^2}{4}){\rm d}x\\ &=8\int^2_{-2}\frac{1}{x^2+4}{\rm d}x-\frac{1}{4}\int^2_{-2}x^2{\rm d}x\\ &=2\int^2_{-2}\frac{1}{\frac{x^2}{4}+1}{\rm d}x-\frac{1}{4}\int^2_{-2}x^2{\rm d}x\\ Пусть\ u&=\frac{x}{2},{\rm d}u=\frac{1}{2}{\rm d}x\\ S&=4\int^1_{-1}\frac{1}{u^2+1}{\rm d}u-\frac{1}{4}\int^2_{-2}x^2{\rm d}x\\ &=\left.4\arctan x\right|^1_{-1}-\frac{1}{4}\int^2_{-2}x^2{\rm d}x\\ &=2\pi-\frac{1}{4}\int^2_{-2}x^2{\rm d}x\\ &=2\pi+\left.(-\frac{x^3}{12})\right|^2_{-2}\\ &=2\pi-\frac{4}{3} \end{split}\]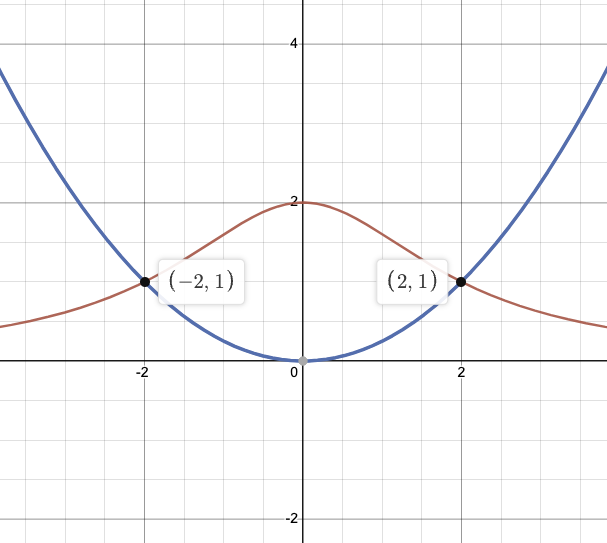
График Функция

b)

\[\begin{split} S\begin{cases} \frac{x^2}{9}-\frac{y^2}{4}=1\\ y=0\\ y=4\\ \end{cases}= S\begin{cases} \frac{y^2}{9}-\frac{x^2}{4}=1\\ x=0\\ x=4\\ \end{cases} \end{split}\]
График Функция
\[\begin{split} &\frac{y^2}{9}-\frac{x^2}{4}=1\\ \Rightarrow&y^2=9+\frac{9x^2}{4}\\ Пусть\ f(x)&=\sqrt{9+\frac{9x^2}{4}},\ то\\ S&=2\int^4_0f(x){\rm d}x\\ &=2\int^4_0\sqrt{9+\frac{9x^2}{4}}{\rm d}x\\ Пучть\ x&=2\tan u,{\rm d}x=2\sec^2 u{\rm d}u\\ S&=4\int^{\arctan 2}_03\sqrt{(\sec^2(u))^3}{\rm d}u\\ &=12\int^{\arctan 2}_0\sqrt{(\sec^2(u))^3}{\rm d}u\\ &=12\int^{\arctan 2}_0\sec^3(u){\rm d}u\\ &=12(\frac{\sin(u)\sec^2(u)}{3-1}+\frac{3-2}{3-1}\int\sec^{3-2}(u){\rm d}u)\\ &=\left.6\tan(u)\sec(u)\right|^{\arctan 2}_0+6\int^{\arctan 2}_0\sec(u){\rm d}u\\ &=12\sqrt{5}+6\int^{\arctan2}_0\frac{\sec^2(u)+\tan(u)\sec(u)}{\tan(u)+\sec(u)}{\rm d}u\\ Пучть\ v&=\tan(u)+\sec(u),{\rm d}v=(\sec^2(u)+\tan(u)\sec(u)){\rm d}u\\ S&=12\sqrt{5}+6\int^{2+\sqrt{5}}_1\frac{1}{v}{\rm d}v\\ &=12\sqrt{5}+\left.6\ln s\right|^{2+\sqrt{5}}_1\\ &=12\sqrt{5}+6\ln(2+\sqrt{5}) \end{split}\]