MainPage/Physics/HomeWork

ДЗ1

1

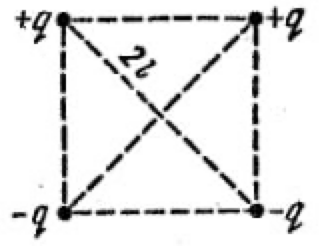
В вершинах квадрата с диагональю $2l$ находятся точечные заряды $q$ и $-q$, как показано на рис 3.1. Найти модуль напряженности электрического поля в точке, отстоящей на расстояние $x$ от центра квадрата и раположенной симметрично относительно вершин квадрата.
如图 3.1 所示，对角线为 $2l$ 的正方形的顶点是点电荷 $q$ 和 $-q$。 求距正方形中心距离 $x$ 且相对于正方形顶点对称的点处的电场强度模量。

Зафиксируем систему координат, взяв точку пересечения диагоналей как начало координат.

\[\vec{E}=\vec{E}_1+\vec{E}_2+\vec{E}_3+\vec{E}_4\\=\frac{q}{4\pi\varepsilon_0}\cdot\frac{l\vec{i}+x\vec{k}}{(l^2+x^2)^{\frac{3}{2}}}+\frac{-q}{4\pi\varepsilon_0}\cdot\frac{-l\vec{i}+x\vec{k}}{(l^2+x^2)^{\frac{3}{2}}}+\frac{-q}{4\pi\varepsilon_0}\cdot\frac{l\vec{j}+x\vec{k}}{(l^2+x^2)^{\frac{3}{2}}}+\frac{q}{4\pi\varepsilon_0}\cdot\frac{-l\vec{j}+x\vec{k}}{(l^2+x^2)^{\frac{3}{2}}}\\ =\frac{q}{4\pi\varepsilon_0(l^2+x^2)^{\frac{3}{2}}}(2l\vec{i}-2l\vec{j})=\frac{2\sqrt{2}ql}{4\pi\varepsilon_0(l^2+x^2)^{\frac{3}{2}}}\]

где $\vec{k}$ - нормальное направление, выходящее из плоскости фигуры.

2

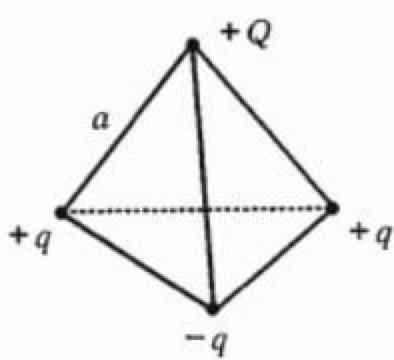
В вершинах тетраэдра расположены четыре заряда (см. рис.). Сторона тетраэдра $a$ Определить силу, действуюшую на заряд $Q$. Заряды считать известными.
四面体的顶点有四个电荷（见图）。 四面体 $a$ 的一侧。 确定作用在电荷 $Q$ 上的力。 假定费用是已知的。

\[\vec{F}=\vec{F_1}+\vec{F_2}+\vec{F_3}\\ F_1=F_2=F_3=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \begin{cases} \vec{F_1}_{x}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\frac{\sqrt{3}}{6}a}{a}=\frac{1}{8\sqrt{3}\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \vec{F_1}_{y}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{0.5a}{a}=\frac{1}{8\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \vec{F_1}_{z}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\sqrt{\frac{2}{3}}a}{a}\\ \end{cases}\\ \begin{cases} \vec{F_2}_{x}=\vec{F_1}_{x}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\frac{\sqrt{3}}{6}a}{a}=\frac{1}{8\sqrt{3}\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \vec{F_2}_{y}=-\vec{F_1}_{y}=-\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{0.5a}{a}=-\frac{1}{8\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \vec{F_2}_{z}=\vec{F_1}_{z}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\sqrt{\frac{2}{3}}a}{a}\\ \end{cases}\\ \begin{cases} \vec{F_3}_{x}=2\vec{F_1}_{x}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\sqrt{3}}{3}\\ \vec{F_3}_{y}=0\\ \vec{F_3}_{z}=-\vec{F_1}_{z}=-\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\sqrt{\frac{2}{3}}a}{a}\\ \end{cases}\\ \begin{cases} \vec{F}_{x}=3\vec{F_1}_{x}=\frac{3}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\frac{\sqrt{3}}{6}a}{a}=\frac{1}{8\sqrt{3}\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\\ \vec{F}_{y}=0\\ \vec{F}_{z}=\vec{F_1}_{z}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\frac{\sqrt{\frac{2}{3}}a}{a}\\ \end{cases}\\ F=\sqrt{F_x^2+F_y^2+F_z^2}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\sqrt{(\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}})^2+\frac{2}{3}}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{Qq}{a^2}\cdot\sqrt{2}\]

ДЗ2

1

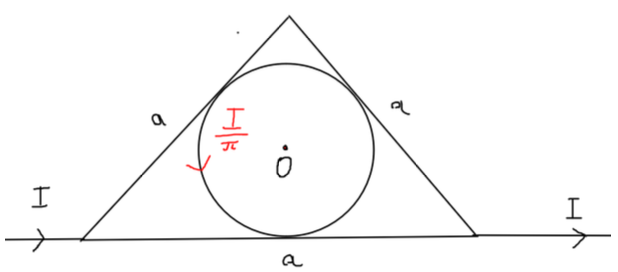
Найти вектор магнитной индукции в точке $O$, которая является центром вписанной окружности в равносторонний треугольник со стороной a. В вершину треугольника втекает ток $I$ По окружности течет независимый ток $\frac{1}{\pi}$. Взаимодействием проводов треугольника и окружности пренебречь.

2

Проводящее кольцо радиуса a вращаются вокруг диаметра с постоянной угловой скоростью $\omega$. В момент времени $t = 0$ включается внешнее однородное магнитное поле $B(t) = B_0\sin(\omega t)$ перпендикулярное плоскости кольца (частота изменения поля такая же как угловая скорость вращения кольца). Найти величину ЭДС электромагнитной индукции и направление индукционного тока.

3

Найти $B, H$ в каждой из трех областей, если система представляет из себя кольцо с током $I$ и радиусом $R$. На расстояние 𝑎 от кольца находится бесконечная проводящая тонкая плоскость с линейной плотностью тока $i$, на расстояние 𝑎 от этой плоскости находится такая же, только с другим направлением линейной плотности $i$. Область 1 и 3 заполнена магнетиком с магнитной проницаемостью $\mu$.