MainPage/Physics/Lab1.04
Лабораторная работа No 1.04
ИССЛЕДОВАНИЕ РАВНОУСКОРЕННОГО ВРАЩЕТЕЛЬНОГО ДВИЖЕНИЯ (МАЯТНИК ОБЕРБЕКА)
Цель работы
- Проверка основного закона динамики вращения.
- Проверка зависимости момента инерции от положения масс относительно оси вращения.
Требуемое оборудование
- Лабораторный стенд для исследования вращательного движения.
- Цифровой секундомер.
Краткое теоретическое введение
Груз $m$ (см. рис. 1.) подвешен на нити, которая перекинута через неподвижный блок Бл и намотана на ступицу Ст крестовины Кр. В ступице закреплены четыре спицы Сп, на каждой из которых размещен груз– утяжелитель $m_ут$. Расстояние $R$ утяжелителей от оси вращения крестовины одинаково для всех утяжелителей. Это расстояние, можно изменять, изменяя тем самым момент инерции крестовины с утяжелителями.
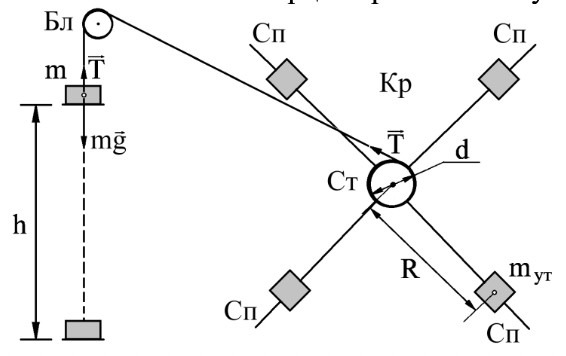
Груз $m$, опускаясь, раскручивает крестовину. Если пренебречь силой сопротивления воздуха, то груз движется равноускорено под действием векторной суммы силы тяжести mg и силы $T$ натяжения нити. Его ускорение $a$ определяется вторым законом Ньютона:
\[ma=mg-T\qquad(1)\]Это ускорение можно вычислить по формуле
\[a=\frac{2h}{t^2}\qquad(2)\]где $h$ расстояние, пройденное грузом за время $t$ от начала движения.
Нить не проскальзывает по ступице, поэтому угловое ускорение $\varepsilon$ крестовины согласовано с линейным ускорением груза. Это угловое ускорение вычисляется по формуле
\[\varepsilon=\frac{2a}{d}\qquad(3)\]где $d$ диаметр ступицы.
Используя уравнение$(1)$ выразим силу натяжения нити:
\[T=m(g-a)\qquad(4)\]и найдем момент этой силы:
\[M=\frac{md}{2}(g-a)\qquad(5)\]Предполагая, что кроме момента силы натяжения на раскручивание крестовины влияет тормозящий момент силы трения, запишем основной закон динамики вращения для крестовины в виде
\[I\varepsilon=M-M_{тр}\qquad(6)\]Здесь $I$ момент инерции крестовины с утяжелителями.
В соответствии с теоремой Штейнера момент инерции крестовины зависит от расстояния между центрами грузов и осью вращения по формуле
\[I=I_0+4m_{уг}К^2\qquad(7)\]где $I_0$ сумма моментов инерции стержней крестовины, момента инерции ступицы и собственных центральных моментов инерции утяжелителей.
Порядок выполнения работы
- Списать или сфотографировать данные об установке на рабочем месте.
- Ознакомится с лабораторным стендом (см. рис.2). Отвернуть рукоятку 2 сцепления крестовин, так чтобы передняя крестовина вращалась независимо от задней.
- Положение каждого утяжелителя на крестовине задается номером риски (канавки на спице), по которой выравнивается грань утяжелителя, ближайшая к оси вращения. Установить все утяжелители на первую риску
- Установить в качестве подвешенного груза каретку 10 с одной шайбой 9 . остальные три шайбы 9 закрепить наверху трубчатой направляющей 6. Измерить три раза время прохождения кареткой из неподвижного положения пути от отметки $h1 = 700мм$ до отметки $h2 = 0$. При этом $h = h1 – h2= 700мм$. Массу m1 каретки с одной шайбой и результаты измерения времени t1, t2, t3 занести в соответствующие ячейки таблицы 1.
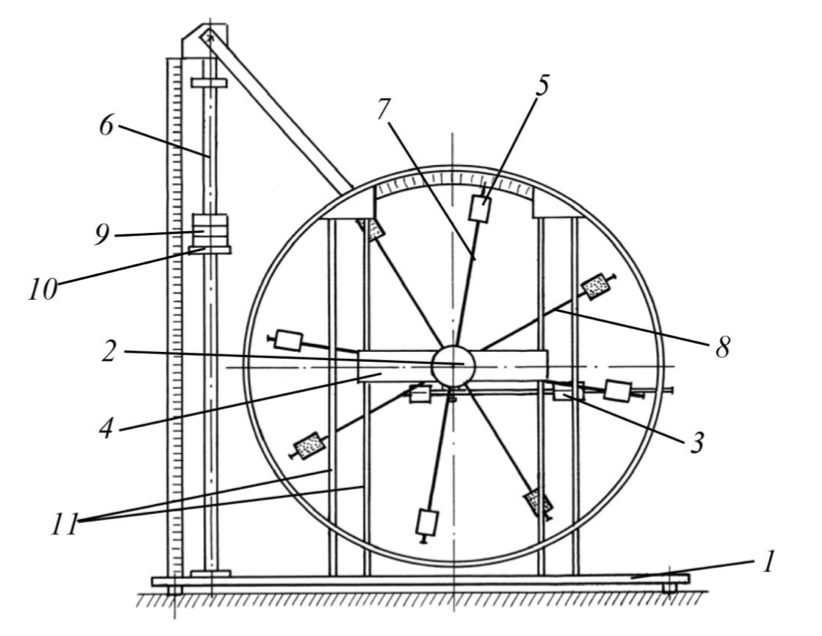
- основание
- рукоятка сцепления крестовин
- устройство принудительного трения
- поперечина
- груз крестовины
- трубчатая направляющая
- передняя крестовина
- задняя крестовина
- шайбы каретки
- каретка
- система передних стоек
- Не изменяя положение утяжелителей крестовины повторить п. 4 для каретки с двумя шайбами (масса $m_2$), тремя шайбами (масса $m_3$) и четырьмя шайбами (масса $m_4$).
- Повторить измерения пп. 4,5 при положении утяжелителей на второй, третьей, …, шестой рисках.
- Найти среднее время падения гири для всех масс гири и всех положениях утяжелителей на крестовине. Для первого значения $t_{ср}$ рассчитать погрешность среднего значения времени $\Delta t$ .
- Используя найденные значения $t_{ср}$ рассчитать ускорение $a$ груза, угловое ускорение $\varepsilon$ крестовины и момент M силы натяжения нити. Результаты оформить в виде таблицы. Для первых значений $a$, $\varepsilon$ и $M$ вычислить их погрешности и записать соответствующие доверительные интервалы.
- Для каждого положения утяжелителей на крестовине в координатах $M$(ордината) – $\varepsilon$(абсцисса) на одном рисунке нанести точки найденных зависимостей $M(\varepsilon)$. Отметить значения погрешностей $\Delta\varepsilon$ и $\Delta M$, вычисленные в п. 8, у тех точек, для которых они найдены.
- Для каждого положения утяжелителей на основе таблицы $M$ и $\varepsilon$ по методу наименьших квадратов (МНК) рассчитать момент $I$ инерции крестовины с утяжелителями и момент силы трения $M_{тр}$. Из формулы $(6)$ следует, что теоретическая связь между моментом силы натяжения нити и угловым ускорением крестовины описывается уравнением
т.е. зависимость $M(\varepsilon)$ является линейной, а величины $I$ и $M_{тр}$ – коэффициенты этой зависимости. Формулы расчета коэффициентов линейной зависимости по МНК приведены в разделе «6.5. Обработка совместных измерений. Метод наименьших квадратов» пособия «Обработка экспериментальных данных» (см. список литературы).
- Используя вычисленные в п. 10 значения $I$ и $M_{тр}$ , на том же рисунке , что и точки п. 9., построить графики зависимости (8) для всех положений утяжелителей.
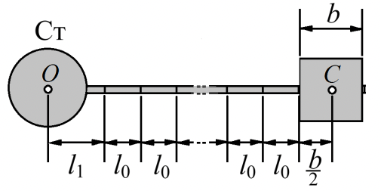
- Для каждого положения утяжелителей найти расстояние (см. рис.3 ) между осью $O$ вращения и центром $С$ утяжелителя по формуле
Здесь
- $l_1$ – расстояние от оси вращения до первой риски;
- $n$ – номер риски, на которой установлены утяжелители;
- $l_0$ – расстояние между соседним рисками;
- $b$ – размер утяжелителя вдоль спицы. Вычислить $R^2$.
- Объединить значения $R, R^2, I$ в таблицу и на основе этой таблицы в координатах $I$(ордината) – $R^2$(абсцисса) отметить экспериментальные точки зависимости $I(R^2)$.
- На основе найденных значений $I$ и $R^2$ с помощью МНК определить значения $I_0$ и $m_{ут}$ , а также их погрешности $\Delta I_0$ и $\Delta m_{ут}$. В соответствии с формулой $(7)$ величина $I_0$ –свободное слагаемое в линейной зависимости $I(R^2)$, $m_{ут}$ – четверть от углового коэффициента наклона этой зависимости. Формулы расчета по МНК коэффициентов линейной зависимости и их погрешностей приведены в разделе «6.5. Обработка совместных измерений. Метод наименьших квадратов» пособия «Обработка экспериментальных данных» (см. список литературы).
- Построить график зависимости (7), используя значения $I_0$ и $m_{ут}$, вычисленные в п. 14, на том же рисунке, что и точки п. 13.
Литература
- Детлаф А. А., Яворский Б. М. Курс физики.— 8-е изд., стер. — М. : Издательский центр “Академия”, 2009 .
- Курепин В.В., Баранов И.В. Обработка экспериментальных данных: Методические указания к лабораторным работам. – СПб, 2003.–57 с.