MainPage/Physics/Lab3.05
Цель работы
- Получить зависимость электрического сопротивления металлического и полупроводникового образцов в диапазоне температур от комнатной до $75^{\circ}C$.
- По результатам п.1 вычислить температурный коэффициент сопротивления металла и ширину запрещенной зоны полупроводника.
Введение
Электрический ток есть направленное движение заряженных частиц - свободных носителей заряда. Без внешнего электрического поля эти носители совершают хаотическое тепловое движение. Средний модуль скорости теплового движения электронов при комнатных температурах порядка $10^5$ м/с. Внешнее электрическое поле действует на носитель заряда с силой
\[\vec{F}=q\vec{E}\qquad(1)\]где $q$ - заряд носителя, $\vec{E}$ - напряженность электрического поля. Таким образом, внешнее поле создает направленное движение носителей заряда - электрический ток с плотностью тока
\[\vec{j}=qn\vec{u}\qquad(2)\]Здесь $n$ - концентрация носителей заряда, $\vec{u}$ - направленная(дрейфовая) скорость носителей. Если ток создается единственным типом носителей (например, электронами), формула (2) дает полную плотность тока в испытуемом образце.
В конденсированных средах носители заряда претерпевают частые столкновения с другими частицами. Это ведет к двум важным следствиям: дрейфовая скорость носителей много меньше средней скорости их теплового движения ($u\ll v$) и пропорциональна силе $\vec{F}$, следовательно, и напряженности поля:
\[\vec{u}=\mu\vec{E}\qquad(3)\]Величину $\mu$ называют подвижностью носителей заряда. В итоге плотность тока оказывается пропорциональной напряженности поля: из (2) и (3) следует
\[\vec{j}=\sigma\vec{E}\qquad(4)\]где $\sigma=qn\mu$ есть параметр конкретного материала - его удельная проводимость. Обратную величину $\rho=\sigma^{-1}$ называют удельным сопротивлением. Соотношение (4) представляет собой дифференциальную (векторную) форму закона Ома.
Зависимость проводимости от температуры принципиально различна для металлов и полупроводников. В металлах практически все валентные электроны свободны - не связаны с каким-либо конкретным атомом, поэтому температура не может заметно изменить концентрацию свободных носителей $n$. Изменение проводимости определяется температурной зависимостью подвижности электронов: $\sigma(T)\sim\mu(T)$.
Подвижность же тем больше, чем реже столкновения носителей со всякого рода дефектами кристаллической решетки. Таковыми являются атомы примеси, отклонения от идеального регулярного расположения атомов в узлах за счет, например, структурных дефектов кристалла или тепловых колебаний решетки. Увеличение с ростом температуры интенсивности тепловых колебаний атомов и хаотической скорости электронов увеличивает частоту столкновений между ними. Это ведет к уменьшению подвижности носителей заряда.
Для не слишком больших интервалов температуры (и не слишком низких температур) удельное сопротивление большинства металлов удовлетворительно описывается линейной зависимостью
\[\rho_M=\rho(1+\alpha t)\qquad(5)\]где $\rho_0$ - удельное сопротивление при температуре $0^\circ C$, $\alpha$ - температурный коэффициент сопротивления. Естественно, так же зависит от температуры и сопротивление любого однородного металлического образца, если весь он имеет эту температуру:
\[R_M=R_0(1+\alpha t)\qquad(6)\]где $R_0$ - сопротивление данного образца при при температуре $0^\circ C$. Пример данной зависимости приведен на рис.1 линией $R_M$.
По данным прямых измерений из формулы (6) легко найти температурный коэффициент сопротивления металла
\[\alpha=\frac{1}{R_0}\cdot\frac{\Delta R}{\Delta t}\qquad(7)\]При этом коэффициент 𝑅0 определяют прямым измерением или экстраполяцией (продлением) линейной зависимости $R=R(t)$ к температуре $t=0^\circ C$.
В полупроводнике валентные электроны связаны с ядрами атомов значительно сильнее, чем в металле. «Оторваться» от атома и превратиться в электрон проводимости могут лишь те из них, которые обладают избыточной энергией, большей некоторого значения $E_g$, которое называют шириной запрещенной зоны. В т.н. собственном полупроводнике (без присутствия в кристаллической решетке примесных атомов иного химического элемента), который является объектом данной лабораторной работы, разрыв каждой связи приводит к образованию пары электрон-дырка (разорванная межатомная связь). Дырки, так как они являются свободными носителями положительного элементарного заряда ($+e$) в отличии от электронов, перемещаются в направлении внешнего электрического поля. Полная плотность тока в полупроводнике складывается из плотностей электронного и дырочного токов: $\vec{j}=\vec{j}-+\vec{j}+$ . Следовательно, удельная проводимость
\[\sigma_П=en(\mu_-+\mu_+)\qquad(8)\]так как в собственном полупроводнике концентрации электронов и дырок одинаковы $(n_-=n_+=n)$, а подвижности $\mu_-$ и $\mu_+$ различны. Но подвижности носителей заряда зависят от температуры существенно слабее, чем их концентрации, и поэтому для полупроводника можно приближенно считать $\sigma_П(T)\sim n(T)$.
Разрыв связей (генерация свободных носителей) достигается за счет энергии тепловых колебаний атомов. Среднее ее значение порядка $kT$ ($k$ - постоянная Больцмана; при комнатной температуре $kT\approx4\cdot10^{-21} Дж \approx 2.5\cdot10^{-2} эВ$). Процесс генерации носителей сопровождается обратным процессом рекомбинации электронов проводимости с дырками. Равновесие наступает, когда средняя частота актов рекомбинации равна средней частоте актов генерации. Расчет дает, что равновесная концентрация свободных носителей при этом
\[n\sim \exp(-\frac{E_g}{2kT})\qquad(9)\]Следовательно, удельная проводимость полупроводника зависит от температуры экспоненциальным образом:
\[\sigma_П\sim\exp(-\frac{E_g}{2kT})\qquad(10)\]а удельное сопротивление будет равно
\[\rho_П=\frac{1}{\sigma_П}=\rho_m\exp(\frac{E_g}{2kT})\qquad(11)\]где $\rho m$ - предел к которому стремится значение удельного сопротивления полупроводника при повышении температуры.
Если однородный полупроводниковый образец весь имеет температуру $T$, то зависимость его сопротивления от этой температуры можно описать формулой
\[R_П=R_m\exp(\frac{E_g}{2kT})\qquad(12)\]Логарифмирование соотношения (12) позволяет представить зависимость сопротивления собственного полупроводника от температуры в более простом виде:
\[\ln(R_П)=\ln(R_m)+\frac{E_g}{2kT}\qquad(13)\]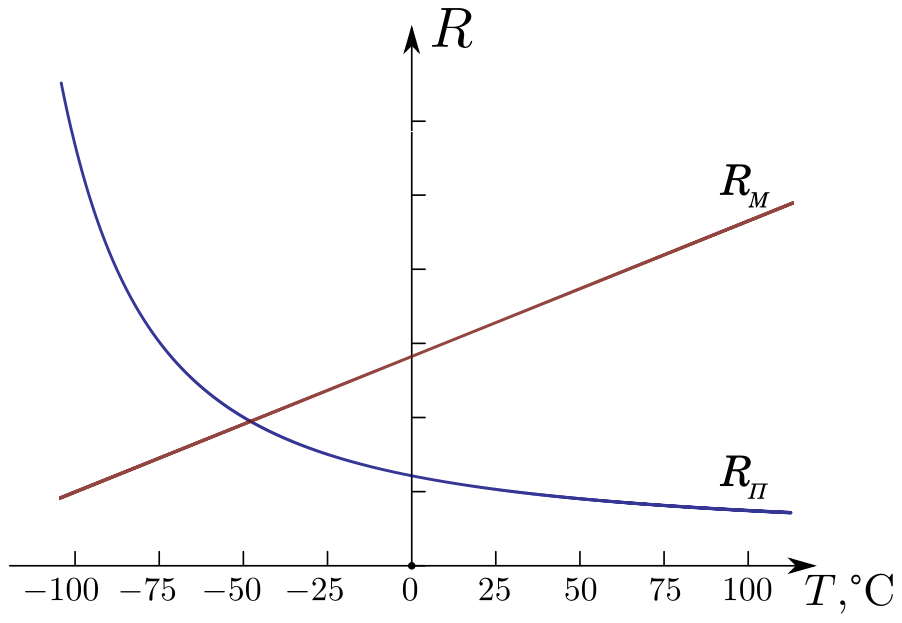
РИС. 1. Зависимость электрического сопротивления металла и собственного полупроводника от температуры
Хорошо видна разница между металлом и полупроводником: сопротивление металла по мере повышения температуры растет, сопротивление полупроводника - падает. Для металла сопротивление линейно зависит от температуры (формула (6), линия $R_M$ на рис.1), а для полупроводника линейно связаны логарифм сопротивления и величина, обратная температуре (формула (13)), следовательно по результатам измерений сопротивления образца из полупроводника можно найти ширину его запрещенной зоны, как угловой коэффициент в зависимости логарифма сопротивления от величины $(2kT)^{-1}$
\[E_g=2k\cdot\frac{\Delta\ln(R_П)}{\Delta(1/T)}\qquad(14)\]Лабораторная установка
Общий вид лабораторной установки показан на рис.2. Она состоит из стенда «С3-ТТ01» с объектами изучения - металлическим и полупроводниковым образцами, генератора ГН1 и амперметра-вольтметра АВ1, соединенных проводниками. На корпусе стенда схематично изображены элементы электрической цепи.

РИС. 2. Общий вид лабораторной установки
Принципиальная электрическая схема установки представлена на рис. 3. Одновременно измеряя напряжение на объекте исследования и ток через него, можно найти его сопротивление с помощью закона Ома для участка цепи $R=U/I$.
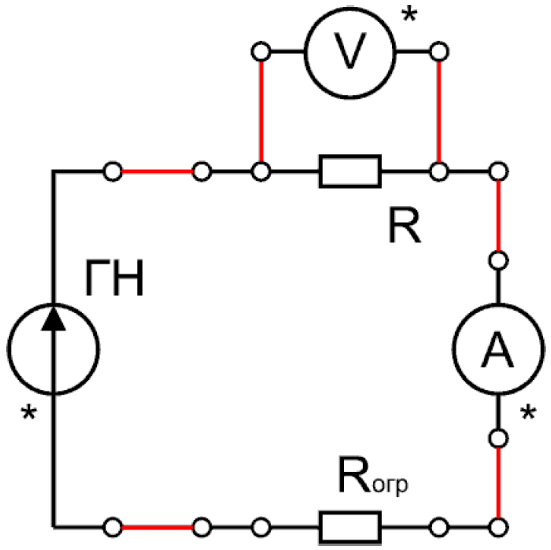
РИС. 3. Принципиальная электрическая схема установки
Нагреватель с системой термостабилизации и измерения текущей температуры объекта находится внутри стенда «С3-ТТ01». Также в корпусе стенда расположен вентилятор, необходимый для более быстрого охлаждения образца.
Дополнительный резистор $R_{огр}$ = 680 Ом, подключаемый последовательно с объектом, необходим в связи с тем, что при нагревании сопротивление полупроводникового образца может уменьшиться в несколько раз, и общее сопротивление схемы будет слишком малым по сравнению с постоянным по величине внутренним сопротивлением источника ЭДС. Для проведения измерений с металлическим образцом отсутствует необходимость подключения $R_{огр}$, но в схеме оно остается из соображений унификации.
Проведение измерений
Задание 1. Изучение полупроводникового образца
- Перед включением проверьте правильность соединения элементов электрической схемы. В цепи должен находиться элемент $R_1$ - полупроводниковое сопротивление.
- Обратите внимание, чтобы регуляторы выходного напряжения генератора (в левой части лицевой панели прибора) и температуры образца (на стенде) находились в крайнем левом положении (т.е. был повернуты против часовой стрелки до упора).
- Кнопки выбора режима измерений на амперметре-вольтметре АВ1 должны находится в т.н. «отжатом» положении, в этом случае прибор обеспечивает измерение постоянных токов и напряжений. Кнопка подключения внутреннего сопротивления генератора ГН1 также должна находится в «отжатом» положении.
- Включите приборы АВ1 и ГН1 с помощью красных кнопок «Сеть» на корпусах приборов. Установите на амперметре диапазон измеряемых токов 0 ÷ 2000 мкА, а на вольтметре диапазон измеряемых напряжений 0÷2 В.
- Аккуратным поворотом по часовой стрелке регулятора выходного напряжения установите значение силы тока, протекающего через образец в интервале 1000÷1400 мкА.
- Убедившись в стабильности показаний всех приборов (в т.ч. электронного термометра на стенде) запишите в Таблицу 1 значения: температуры (в кельвинах), силы тока (в мкА с точностью до единиц), напряжения (в вольтах, с точностью до тысячных долей).
- Включите подогрев образца, плавным поворотом по часовой стрелке установив регулятор температуры между делениями шкалы 370 K и 390 K. При этом должен начать светиться красный индикаторный светодиод «Нагрев» на панели стенда «С3-ТТ01». Нагрев образца при этом происходит в непрерывном режиме и его температура монотонно начнет расти.
Задание 2. Изучение металлического образца
- Не выключая нагрев, замените объект измерений - подключив элемент $R_2$ (металлический резистор) вместо элемента $R_1$. Для этого следует переключить провод идущий от ограничительного резистора $R_{огр}$ на одну позицию ниже и подключить вольтметр параллельно элементу $R_2$.
- Рабочие диапазоны измерительных приборов остаются прежними.
- Отрегулируйте выходное напряжение генератора так, чтобы ток через образец находился в диапазоне 1200÷1500 мкА.
- Плавным поворотом регулятора температуры против часовой стрелки до упора выключите подогрев термостабилизируемой площадки с образцами. Ее температура начнет уменьшатся вследствие теплообмена с окружающей средой.
- Начиная с $ = 350 ÷ 355$ K запишите в Таблицу 2 протокола текущие значения температуры, тока и напряжения на металлическом образце.
- Выждав время, необходимое для уменьшения температуры на $\Delta T = 3÷5$ 𝐾, повторите действия из предыдущего пункта, заполняя таким образом рабочую таблицу до достижения температуры близкой к комнатной $T = 295 ÷ 300$ 𝐾.
- До значения $\approx 340$ K температура образца будет опускаться в достаточно удобном темпе для того, чтобы успевать записывать показания приборов. При меньших температурах для ускорения процесса измерений можно тумблером на лицевой панели стенда кратковременно (на 5-10 сек) включать вентилятор для увеличения конвективного теплообмена. Обратите внимание, во время снятия показаний приборов вентилятор должен быть выключен.
- После завершения процесса измерений следует в невыключенном состоянии сдать лабораторную установку дежурному инженеру и получить его подпись на стандартном бланке протоколотчета.
Обработка результатов измерений
- Рассчитайте и запишите в рабочие таблицы значения сопротивления объектов исследования при всех температурах.
- По данным Таблицы 1 рассчитайте значения натурального логарифма сопротивления полупроводника и величину обратной абсолютной температуры. По результатам расчетов постройте график соответствующей зависимости $\ln(R)=\ln(R)(\frac{1}{T})$. Качественно оцените линейность полученного графика.
- По данным Таблицы 2 постройте на масштабной миллиметровой бумаге график зависимости сопротивления металла от температуры в шкале Цельсия $R_M = R_M(t)$. Интервалы величин сопротивления и температуры на осях выберите в соответствии с диапазонами изменения этих величин в проведенных измерениях. Качественно оцените линейность полученного графика.
- Для определения величины температурного коэффициента сопротивления металла разделите все точки в Таблице 2 на пары, в которых значения отстоят друг от друга на примерно одинаковое максимальное расстояние. Например, если в таблице имеется 12 независимых значений, то первая точка объединяется в пару с седьмой, вторая с восьмой, и так далее. Поскольку мы считаем, что зависимость сопротивления металла от температуры имеет линейный характер, то для каждой пары значений можно написать систему линейных уравнений:
После исключения неизвестной величины $R_0$ из этой системы получаем рабочую формулу для нахождения $\alpha$:
\[\alpha_{ij}=\frac{R_i-R_j}{R_j\cdot t_i-R_i\cdot t_j}\qquad(16)\]- После проведения вычислений по формуле (16) со всеми парами значений из Таблицы 2 вы получите набор значений $\alpha$, по которому можно с помощью стандартных формул найти среднее значение $⟨\alpha⟩$ и оценить его погрешность $\Delta\alpha$.
- Аналогичные действия следует провести и при вычислении ширины запрещенной зоны полупроводника. В соответствии с формулой (13) связь между натуральным логарифмом сопротивления полупроводника и обратной температурой является линейной. Разбивая весь массив экспериментальных данных на независимые пары, получаем рабочую формулу для оценки ширины запрещенной зоны полупроводника:
- Найдите среднее значение ширины запрещенной зоны $⟨𝐸𝑔⟩$ и его погрешность $\Delta E_g$. Окончательный результат представьте как в джоулях, так и в электрон-вольтах, учитывая что постоянная Больцмана имеет значение:
- Результаты всех расчетов с указанием погрешностей представьте в отчете в стандартной форме.
- По значению температурного коэффициента сопротивления металла и ширине запрещенной зоны полупроводника с помощью литературных данных идентифицируйте их.
- Сформулируйте выводы по лабораторной работе и запишите их в отчет.
Приложение
| № | T, K | I, мкА | U, B | R, Ом | $\ln R$ | $\frac{10^3}{T}, \frac{1}{K}$ |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| … |
Таблица 1: Полупроводниковый образец
1) Цель работы: какие зависимости, величины хотим получить? 2) Какие величины измеряем, какими будут погрешности? 3) Чем обусловлена разная зависимость проводимости от температуры для металлов и проводников? 4) Какой объект (конденсатор, резистор и т.д.) исследуется?