ITMO-PE

MainPage/Physics/Lab3.13

Цель работы

Провести измерения направления суммарного магнитного поля, создаваемого Землей и системой катушек Гельмгольца.
Определить горизонтальную составляющую магнитного поля Земли.

Введение

В 1600 г в своем шеститомном трактате «О магните, магнитных телах и большом магните — Земле» английский ученый Уильям Гильберт (William Gilbert) впервые предположил, что Земля является магнитом, ось которого не совпадает с осью ее вращения. В любой точке пространства, окружающего Землю, и на её поверхности обнаруживается действие магнитных сил. Подвешенная на нити или укрепленная на острие магнитная стрелка устанавливается в каждой точке вблизи земной поверхности определенным образом – приблизительно в направлении с севера на юг. Этот основной факт доказывает существование магнитного поля Земли.

В 1635 г. английский математик Генри Геллибранд (Henry Gellibrand), показал что поле земного магнита медленно меняется, а знаменитый астроном и математик Эдмунд Галлей (Edmond Halley) провел первую в мире магнитную съемку океанов и создал в 1702 г. первые мировые магнитные карты. В 1835 г. Иоганн Карл Фридрих Гаусс (Johann Carl Friedrich Gauß) провел сферический гармонический анализ магнитного поля Земли. Также он создал первую в мире магнитную обсерваторию в Геттингене и изобрёл униполярный и бифилярный магнитометры.

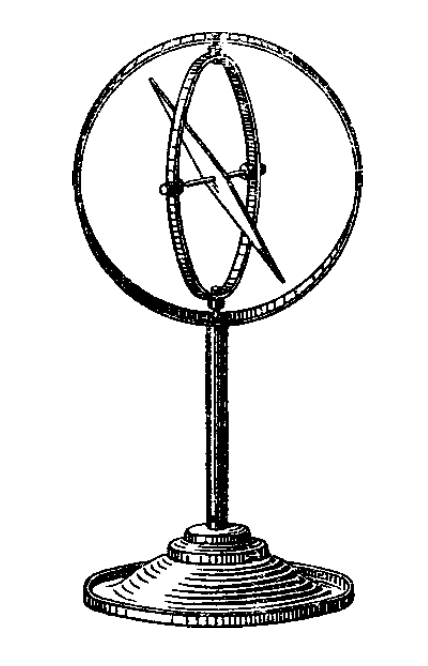
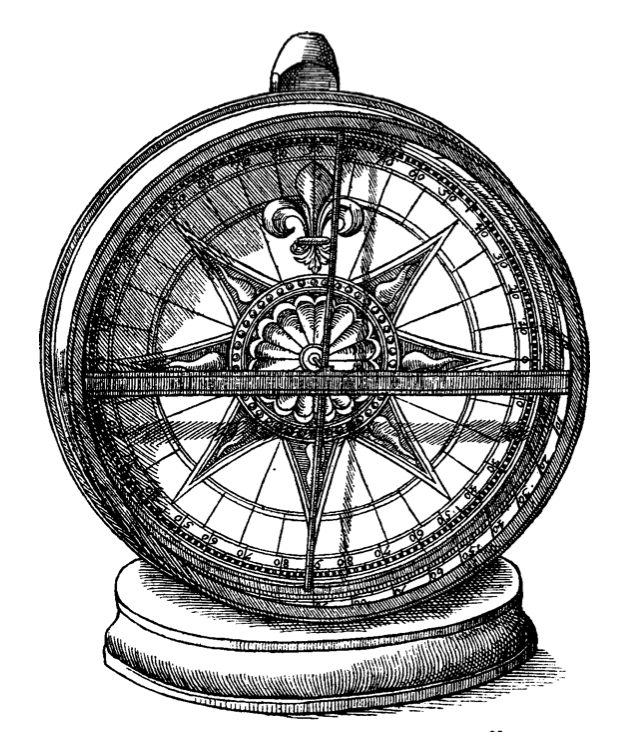
Представление о направлении вектора индукции магнитного поля Земли в данной точке можно получить, укрепив магнитную стрелку так, чтобы она могла свободно вращаться и вокруг вертикальной, и вокруг горизонтальной оси. Это можно осуществить, например, с помощью так называемого карданова подвеса, показанного на Pис. 1, или же специального прибора - деклинометра (Рис. 2). Стрелка устанавливается при этом по направлению вектора индукции магнитного поля Земли.

РИС. 1. Простейший магнитометр - намагниченная стрелка в кардановом подвесе

РИС. 2. Магнитометр-деклинометр XVII в.

Земное магнитное поле имеет такой вид, как будто земной шар представляет собой магнит с осью, направленной приблизительно с севера на юг (см. рис. 3).

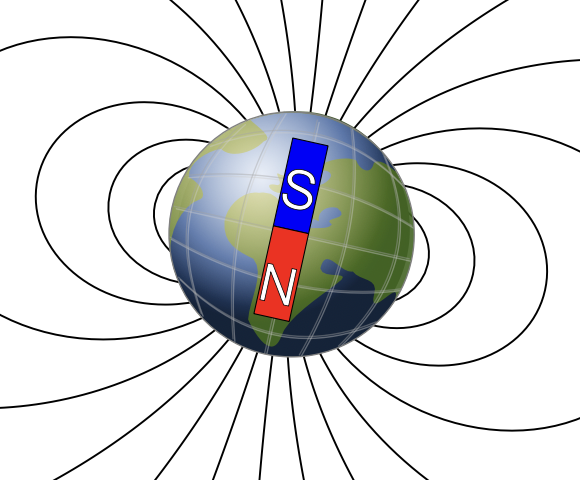
РИС. 3. Общий вид магнитного поля Земли

Земля обладает магнитным полем, которое приблизительно имеет такой вид, как будто земной шар представляет собой магнит с осью, направленной с севера на юг. Причем «южный» (S) и «северный» (N) полюса этого магнита располагаются вблизи северного и южного географических полюсов, соответственно (см. рис. 6). По данной причине стрелка магнитного компаса лишь примерно направлена на север. Ее направление отличается от истинного указания на север углом, называемым склонением. Более того, геомагнитное поле (особенно в приполярных областях) имеет существенную вертикальную составляющую, что приводит к тому что намагниченная игла, подвешенная в центре ее масс, в общем случае не принимает горизонтального (параллельного поверхности Земли) положения. Как правило, в северном полушарии ее 𝑁-полюс опускается вниз на угол, называемый наклонением.

Для геомагнитного поля Земли определяют две пары полюсов: геомагнитные и истинные магнитные полюса. Геомагнитные полюса (дипольные) - это точки пересечения земной поверхности осью магнитного диполя, гипотетически расположенного в центре Земли. В свою очередь, истинные магнитные полюса - это точки, в которых направление силовых линий магнитного поля перпендикулярно земной поверхности.

Согласно данным Международной модели главного магнитного поля Земли в 2020 году северный геомагнитный полюс находился точке, лежащей на 80,7° северной широты и 72,7° западной долготы.

Более того, если положения географических полюсов постоянны, то геомагнитное поле со временем изменяется. Его полюса дрейфуют, совершая перемещения по земной поверхности со скоростью в несколько десятков километров в год. Также меняется магнитный дипольный момент Земли (в настоящую геомагнитную эпоху он почти линейно уменьшается). Даже на протяжении одних суток магнитный полюс не стоит на месте, а совершает небольшие смещения вокруг некоторой средней точки. Причиной таких быстрых перемещений является Солнце. Потоки заряженных частиц от него (солнечный ветер) входят в магнитосферу Земли и порождают в земной ионосфере электрические токи. Те, в свою очередь, порождают вторичные магнитные поля, которые возмущают геомагнитное поле.

Элементы геомагнетизма

В настоящее время употребляются следующие определения:

Истинные магнитные полюса Земли - точки на земной поверхности, где магнитная стрелка располагается вертикально.
Геомагнитные полюсы - точки пересечения магнитной оси Земли с ее поверхностью. Приблизительно можно считать, что Земля является однородно намагниченным шаром, магнитная ось которого составляет угол 10° с осью ее вращения.
Геомагнитный меридиан - проекция силовой линии магнитного поля Земли на земную поверхность.
Магнитный экватор - геометрическое место точек на земной поверхности, в которых магнитная стрелка располагается горизонтально. Магнитный экватор не совпадает с географическим экватором.
Геомагнитная широта - угловое расстояние от геомагнитного экватора до рассматриваемой точки земной поверхности. Геомагнитная широта отсчитывается вдоль большого круга, проходящего через данную точку и геомагнитные полюсы.

Через магнитные полюса Земли можно провести линии больших кругов - магнитные меридианы, перпендикулярно к ним линию большого круга - магнитный экватор, и параллельно последнему, линии малых кругов - магнитные параллели. Таким образом, каждой точке на Земле будут соответствовать не только географические, но и магнитные координаты.

Полное представление о величине магнитного поля Земли в данной точке можно получить, зная значения трех величин, называемых элементами земного магнетизма: значение горизонтальной составляющей индукции магнитного поля, значения магнитного склонения и наклонения.

РИС. 4. Элементы земного магнетизма

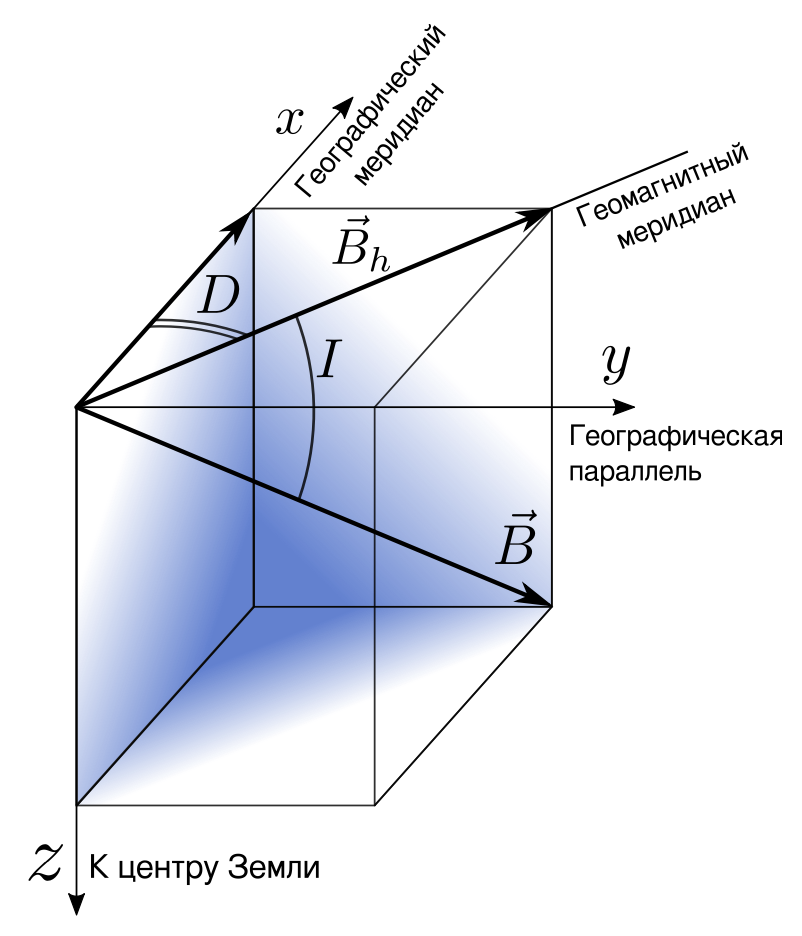
Магнитное склонение (на рис. 4 - $D$) - угол между географическим и магнитным меридианами в точке земной поверхности. Магнитное склонение считается положительным, если северный конец магнитной стрелки отклонен к востоку от географического меридиана, и отрицательным - если к западу. Значение магнитного склонения указывается на магнитных картах и используется для определения истинного меридиана по показанию магнитного компаса. Для Санкт-Петербурга и Ленинградской области величина магнитного склонения на данный момент равна +11°12′ (восточное склонение). Магнитное наклонение (на рис. 4 - $I$) — угол между магнитной силовой линией и горизонтальной плоскостью. На магнитных полюсах Земли, а также в районах крупных магнитных аномалий магнитное наклонение равно 90°.

Для определения численного значения индукции магнитного поля в данной точке рассмотрим плоскость геомагнитного меридиана данного места. Разложим вектор магнитной индукции, лежащий в этой плоскости, на две составляющие: горизонтальную $B_h$ и вертикальную $B_v$ (рис. 4а ). Зная угол наклонения $\theta$ и величину одной из составляющих, мы можем легко вычислить величину другой составляющей или самого вектора $B$. Если известна величина горизонтальной компоненты $B_h$, то из прямоугольного треугольника можно найти вертикальную составляющую:

\[B_v=B_h\cdot tg(\theta).\qquad(1)\]

Также легко можно определить модуль вектора индукции магнит- ного поля:

\[B=\sqrt{B_h^2+B_v^2}\]

Для определения горизонтальной составляющей индукции магнитного поля Земли можно рассмотреть суперпозицию какого-нибудь пробного магнитного поля, индукция которого в данной точке направлена горизонтально (например, поля системы катушек Гельмгольца, см. далее), и горизонтальной составляющей магнитного поля Земли (рис. 5). Угол между направлением пробного поля $\vec{B}_c$ и земного магнитного поля $\vec{B}_h$ обозначим как $\varphi$, а угол между направлением результирующего поля и земного магнитного поля - $\alpha$. Рассматривая треугольник, составленный из этих трех векторов и используя теорему синусов, легко получить:

\[\frac{\sin(\alpha)}{\sin(\varphi-\alpha)}=\frac{B_h}{B_c}\qquad(3)\]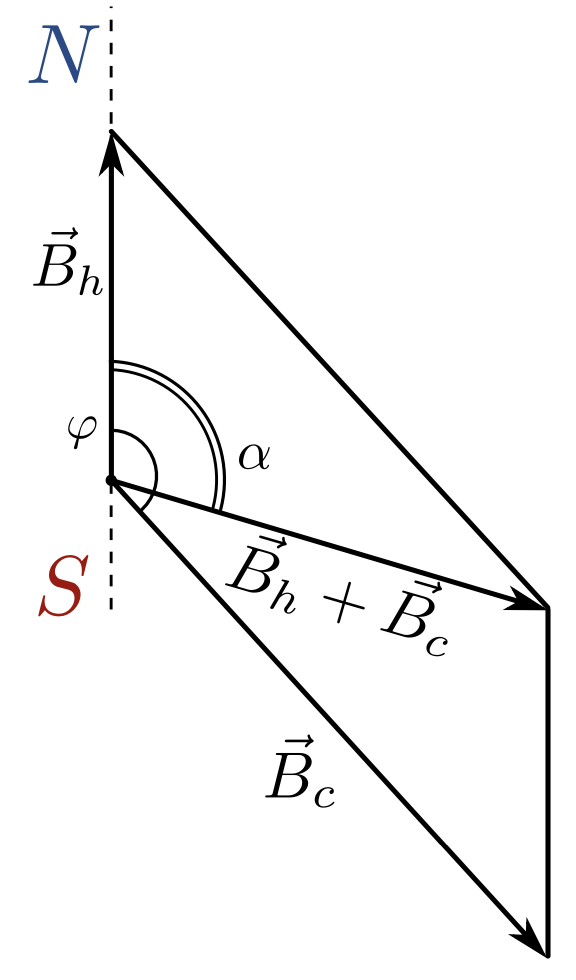

РИС. 5. Проекции векторов магнитного полей Земли 𝐵⃗_h и катушек Гельмгольца 𝐵⃗_c вгоризонтальнойплоскости

Тогда, измерив значения углов $\alpha$ и $\varphi$, для каждого значения пробного магнитного поля $B_c$, можно построить линейную зависимость:

\[B_c=B_h\cdot\frac{\sin(\alpha)}{\sin(\varphi-\alpha)}\qquad(4)\]

где угловой коэффициент - искомое значение горизонтальной составляющей индукции магнитного поля Земли $B_h$.

Магнитное поле колец Гельмгольца

Катушками (кольцами) Гельмгольца называется система, состоящая из двух одинаковых тонких катушек (колец), расположенных соосно на расстоянии, равном их радиусу. В пространстве между катушками создается почти однородное магнитное поле, индукцию которого можно найти по формуле:

\[B=\mu_0(\frac{4}{5})^{\frac{3}{2}}\frac{In}{R}\qquad(5)\]

где $n$ – число витков в каждой катушке, $I$ – сила тока, $R$ – средний радиус каждой катушки.

Получим формулу (5) магнитной индукции в центре колец Гельмгольца. Рассмотрим магнитное поле, создаваемое током, протекающим по тонкому контуру, имеющему форму окружности радиуса $R$ (круговой ток).

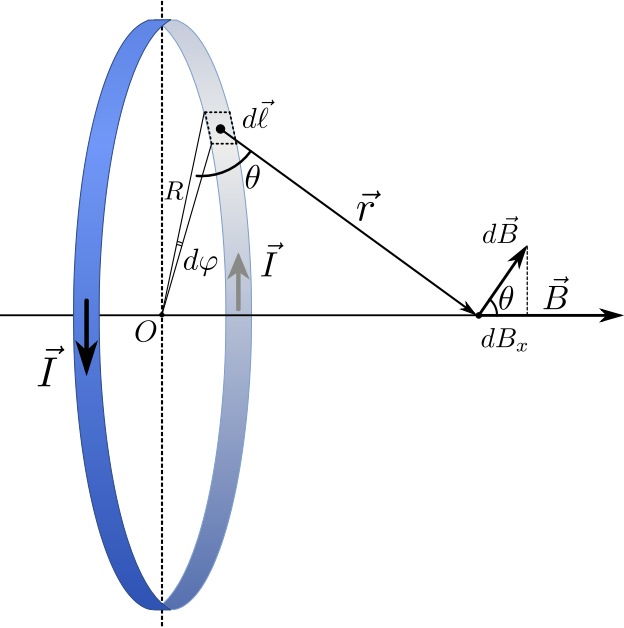
РИС. 6. Магнитное поле на оси кольца с током

Найдем магнитную индукцию $B$ на оси кругового тока на расстоянии $x$ от центра контура (см. рис. 2). Элемент тока ${\rm d}l$ создает в рассматриваемой точке согласно закону Био–Савара–Лапласа индукцию, модуль которой равен

\[{\rm d}B=\frac{\mu_0}{4\pi}\frac{I{\rm d}l}{r^2}\qquad(6)\]

От всех элементов тока будет образовываться конус векторов ${\rm d}\vec{B}$. Из соображений осевой симметрии можно заключить, что результирующий вектор в точке будет направлен параллельно оси 𝑂𝑥 вправо. Это значит, что для нахождения модуля этого вектора необходимо сложить проекции векторов ${\rm d}B$ на ось $O_x$:

\[{\rm d}B_x={\rm d}B\cos\theta=\frac{\mu_0}{4\pi}\frac{I{\rm d}l}{r^2}\frac{R}{r}\qquad(7)\]

Интегрируя выражение (7) по всему токовому контуру и учитывая, что $r=\sqrt{x^2+R^2}$ и ${\rm d}l=R{\rm d}\varphi$, получим:

\[B(x)=\frac{\mu_0I}{2}\frac{R^2}{(x^2+R^2)^{\frac{3}{2}}}\qquad(8)\]

Формула (9) определяет величину магнитной индукции на оси одного кругового тока. Рассмотрим далее систему из двух кольцевых проводников одинакового радиуса $R$, центры которых расположены на оси $O_x на расстоянии $R$ друг от друга, а плоскости в которых лежат токи параллельны между собой. Поместим начало координат на равном удалении от плоскостей колец. Если токи в каждом кольце одинаково направлены и равны по величине, то индукция магнитного поля в начале координат будет в два раза больше индукции поля одного кольца, рассчитанного на расстоянии $x=\frac{R}{2}$ от его плоскости. В реальной ситуации, такую систему колец использовать сложно, так как величина тока, необходимая для получения даже небольших полей будет слишком велика. Поэтому для создания однородных поля используют катушки с большим числом витков, которое обозначим $n$. Тогда результирующее поле в начале координат будет равно

\[B_c=\frac{\mu_0InR^2}{((\frac{R}{2})^{2}+R^2)^{\frac{3}{2}}}\qquad(9)\]

Лабораторная установка

Лабораторная установка (рис. 7) включает в себя последовательно соединенные кольца Гельмгольца с компасом в центральной части, источник питания со встроенным амперметром и токоограничивающее сопротивление. Кольца Гельмгольца смонтированы на устойчивом основании и расположены параллельно друг другу.

РИС. 7. Параметры установки: R = 0,15 м – радиус катушек; n = 100 – число витков в каждой из катушек

Порядок проведения измерений

Перед проведением измерений убедитесь, кольца Гельмгольца расположены на достаточном удалении от источника питания и других приборов (в т.ч. мобильных телефонов и ноутбуков), которые могут иметь собственные электромагнитные поля.
Не включая источник питания, соберите лабораторную установку, соединив прилагающимися проводами все ее элементы. Проверьте, что ток будет протекать по обеим катушкам в одном и том же направлении.
Ориентируйте основание колец на рабочем столе таким образом, чтобы вектор магнитного поля катушек составлял с направлением магнитной стрелки компаса максимально тупой ≊ 160° угол. Для определения направления магнитного поля катушек обратите внимание на полярность их подключения к источнику и используйте правило правой руки.
Отъюстируйте положение компаса в горизонтальной плоскости. Его стрелка должна свободно вращаться вокруг вертикальной оси, не касаясь своими концами внутренней поверхности корпуса.
Запишите в протокол значение угла, который образован плоскостью магнитного меридиана (в ней расположена стрелка компаса) и направлением оси катушек - это угол $\varphi$ на рис. 5.
Перед включением источника установите регулятор силы тока на его лицевой панели в крайнее левое положение. Включите источник.
Плавно увеличивая силу тока в цепи, добейтесь отклонения стрелки компаса от ее исходного положения на угол $\alpha_1 = 10°$. Аккуратно постукивая по основанию на котором расположен компас, убедитесь что положение стрелки является стационарным и устойчивым. Запишите значение угла $\alpha$ и соответствующую ему силу тока в катушках в рабочую таблицу протокола (см. Приложение).
Верните регулятор силы тока на источнике в исходное (нулевое) положение и повторите настройку на угол $\alpha_1$ еще дважды, записывая в таблицу соответствующие величины сил тока.
Проведите аналогичные измерения во всем доступном диапазоне значений угла $\alpha < \varphi$, с шагом $\Delta\alpha = 10°$, а именно $\alpha_2 = 20°$, $\alpha_3 = 30°$ и т.д. В области малых углов отклонения (примерно до $60°$) может быть удобным подключение дополнительного токоограничивающего сопротивления, которое расположено внутри источника тока: для этого необходимо нажать кнопку $R_{ВН}$ на лицевой панели источника.
Завершив измерения, верните регулятор силы тока в нулевое (крайнее левое) положение, выключите источник. Получите подпись инженера зала на протоколе с результатами прямых измерений.

Обработка результатов измерений

По результатам прямых измерений из Табл. 1 рассчитайте величины средней силы тока в катушках $⟨I⟩$ для каждого значения угла 𝛼𝑖. По формуле (5) найдите величины магнитного поля катушек Гельмгольца $B_c$ для всего набора значений силы тока. Результаты расчетов внесите в рабочую таблицу.
Найдите значения параметров $\gamma_i = \frac{\sin(\alpha_i)}{\sin(\varphi-\alpha_i)}$ для всех углов отклонения стрелки. Постройте график зависимости $B_c = B_c(\gamma_i)$. Правила построения графиков изложены в методическом пособии «Обработка экспериментальных данных». Проанализируйте вид полученной зависимости.
Числовое значение углового коэффициента графика зависимости $B_c = B_c(\gamma_i)$ равно величине магнитного поля Земли. Найдите это значение и оцените его погрешность с помощью метода наименьших квадратов (МНК). Основы данного метода также приведены в методическом пособии «Обработка экспериментальных данных».
Полученное значение индукции магнитного поля Земли с обязательным указанием доверительного интервала приведите в п.12 «Окончательные результаты» вашего отчета по лабораторной работе.
Проведите сравнение результата ваших измерений и расчетов с табличным значением. В отчете необходимо явное указание на источник из которого была получена информация о табличном значении.