MainPage/Physics/Practice
Practice
1.399
Стержень движется равномерно в продольном направлении мимо двух меток $A$ и $B$, расположенных на расстоянии $\Delta x$ друг от друга. Сначала в момент $t_1$ напротив метки $A$ оказался передний конец стержня. Затем напротив метки $B$ в моменты $t_2$ и $t_3$ оказались соответственно передний и задний концы стержня. Найти его собственную длину.
杆沿纵向均匀移动经过两个标记 $A$ 和 $B$,它们之间的距离为 $\Delta x$。首先,在 $t_1$ 时刻,杆的前端与标记 $A$ 相对。然后,分别在 $t_2$ 和 $t_3$ 时刻与标签 $B$ 相对的是杆的前端和后端。找到自己的长度。
Решение
в K системе отчёта, по отношению к которой стержень двигается со скоростью $v$, 4-мерные координаты переднего и заднего концов стержня равны:
\[(t,x_A+v(t-t_1),0,0)\] \[(t,x_B+v(t-t_3),0,0)\]Расстояние между метками $AB$ равно
\[x_B-x_A=\Delta x=v(t_2-t_1)\]Таким оброзом
\[\begin{split} l&=x_A-x_B+v(t_3-t_1)=l_0\sqrt{1-\beta^2}\\ l&=-v(t_2-t_1)+v(t_3-t_1)=l_0\sqrt{1-\frac{v^2}{c^2}}\\ \end{split}\]Заменим $v=\frac{\Delta x}{t_2-t_1}$, получим
\[\frac{\Delta x}{t_2-t_1}(t_3-t_2)=l_0\sqrt{1-\frac{\left(\frac{\Delta x}{t_2-t_1}\right)^2}{c^2}}\]откуда
\[l_0=\Delta x\frac{t_3-t_2}{\sqrt{(t_2-t_1)^2-(\frac{\Delta x}{c})^2}}\]1.284
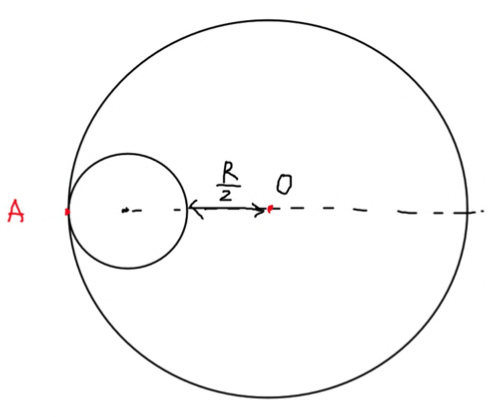
Однородный диск радиуса $R$ имеет круглый вырез (рис. 1). Масса оставшейся (заштрихованной) части диска равна $m$. Найти момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей:
- а) через точку $O$;
- б) через его центр масс.
一个半径为 $R$ 的均匀圆盘有一个圆形缺口(图 1)。圆盘剩余(阴影部分)的质量为 $m$。求这样一个圆盘绕垂直于圆盘平面并通过的轴的转动惯量:
- a) 通过点 $O$;
- b) 通过其质心。
Решение
- a)
Пусть
- $S_B$ - площадь большого диска
- $S_S$ - площадь маленького диска
- $m_B$ - масса большого диска
- $m_S$ - масса большого диска
Очевидно, что
\[\begin{cases} S_B=\pi R^2\\ S_S=\frac{1}{16}\pi R^2\\ \frac{m_B}{m_S}=\frac{S_B}{S_S}=16\\ m_B-m_S=m \end{cases}\Rightarrow \begin{cases} m_B=\frac{16m}{15}\\ m_S=\frac{m}{15}\\ \end{cases}\]Тогда момент инерции через точку $O$
\[\begin{split} J_{BO}&=\frac{1}{2}m_BR^2=\frac{16}{30}mR^2\\ J_{SO}&=\frac{1}{2}m_S\frac{1}{16}R^2+m_S(\frac{3}{4}R)^2=\frac{1}{480}mR^2+\frac{3}{80}mR^2=\frac{19}{480}mR^2\\ J_\Delta&=J_{BO}-J_{SO}=\frac{16}{30}mR^2-\frac{19}{480}mR^2=\frac{79}{160}mR^2 \end{split}\] - b)
Пусть
-
$x_c$ - координат центра масса
\[x_c=\frac{m_Sd_S}{m_\Delta}=\frac{\frac{m}{15}\cdot\frac{3R}{4}}{m_B-m_S}=\frac{R}{20}\]Тогда момент инерции через центр масс
\[\begin{split} J_{BC}&=\frac{1}{2}m_BR^2+m_B(\frac{R}{20})^2=\frac{16}{30}mR^2+\frac{1}{375}mR^2=\frac{67}{125}mR^2\\ J_{SC}&=\frac{1}{2}m_S\frac{1}{16}R^2+m_S(\frac{3}{4}R+\frac{R}{20})^2=\frac{1}{480}mR^2+\frac{16}{375}mR^2=\frac{179}{4000}mR^2\\ J_\Delta&=J_{BO}-J_{SO}=\frac{67}{125}mR^2-\frac{179}{4000}mR^2=\frac{393}{800}mR^2 \end{split}\]
-
1.383
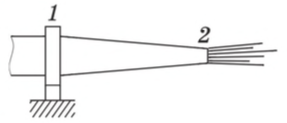
Сечение ствола гидромонитора (рис. 2) меняется от $S_1=50\ см^2$ до $S_2=5.0\ см^2$. Найти модуль и направление горизонтальной силы, возникающей в креплении ствола (сечение $1$), если скорость струи на выходе $v_2=25\ м/с$. Вязкостью пренебречь.
水力监测筒的截面(图 2)从 $S_1=50\ cm^2$ 到 $S_2=5.0\ cm^2$。 如果出口处的射流速度为 $v_2=25\ m/s$,则求出在枪管附件($1$ 部分)中产生的水平力的模量和方向。 忽略粘度。
Решение
\[vS=Const\] \[v_1S_1=v_2S_2\] \[v_1=\frac{v_2S_2}{S_1}=2.5m/s\]Из формулы Бернулли, мы знаем
\[p_1+\frac{1}{2}\rho v_1^2=p_0+\frac{1}{2}\rho v_2^2=Const\]где $p_0$ - атмосферное давление
\[p_1=p_0+\frac{1}{2}\rho v_2^2-\frac{1}{2}\rho v_1^2\] \[F_1=p_1S_1\]4)
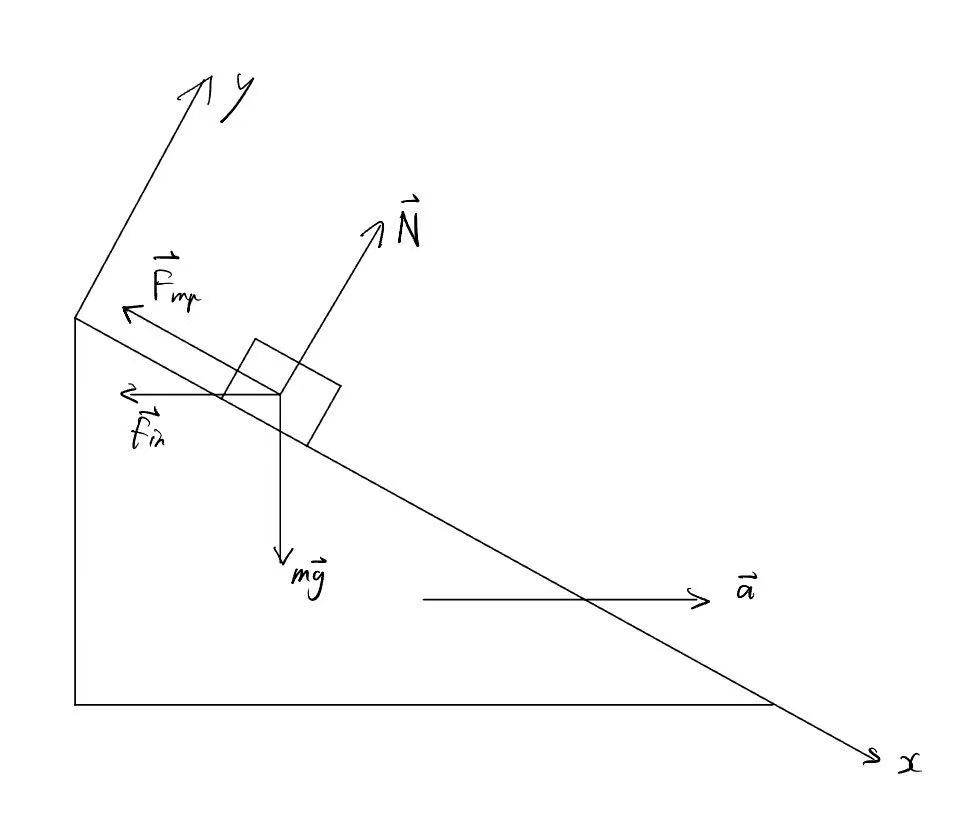
Тело находится в покое на вершине наклонной плоскости. За какое время тело соскользнет с плоскости, если плоскость в момент времени $t_0=0$ начнет двигаться вправо в горизонтальном направлении с ускорением $\vec{a}=1\ м/с^2$? Высота плоскости $h=1м$, угол наклона к горизонту $\alpha=30^\circ$, коэффициент трения между телом и плоскостью $\mu=0.6$.
身体静止在一个斜面的顶部。 如果斜面在时间 $t_0=0$ 开始以加速度 $\vec{a}=1\ m/s^2$ 向右水平方向移动,物体滑离斜面需要多长时间? 斜面的高度为 $h=1m$,与地平线的倾角为 $\alpha=30^\circ$,物体与斜面的摩擦系数为 $\mu=0.6$。
Решение
для тела:
\[m\vec{a}_т=m\vec{g}+\vec{N}+\vec{F}_{тр}+\vec{F}_{in}\]где
- $\vec{a}_{т}$ - ускорение тела
- $\vec{F}_{in}=-m\vec{a}$ - сила инерции
5)
Частица массы $m$ находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты следующим образом $U=\frac{a}{x^{\frac{3}{2}}}-\frac{b}{x^{\frac{1}{2}}}$. Найти период малых колебаний (выполняется Закон Гука ${\rm d}F=-k\cdot{\rm d}x$ - сила возвращающая тело в положение равновесия).
一个质量为 $m$ 的粒子在一维力场中,其势能取决于坐标 $U=\frac{a}{x^{\frac{3}{2}}}-\frac{ b}{x^{ \frac{1}{2}}}$。 找到小振荡的周期(胡克定律 ${\rm d}F=-k\cdot{\rm d}x$ 满足 - 使物体回到平衡位置的力)。
Решение
\[U(x)=\frac{a}{x^{\frac{3}{2}}}-\frac{ b}{x^{ \frac{1}{2}}}\] \[F(x)=-\frac{ {\rm d}U(x)}{ {\rm d}x}=\frac{3}{2}ax^{-\frac{5}{2}}-\frac{1}{2}bx^{-\frac{3}{2}}\] \[F(x)=-k\cdot x\] \[F(x)=-m\omega^2 x\] \[\omega=\sqrt{\frac{k}{m}}\] \[\omega^2=-\frac{F(x)}{mx}=\frac{b}{2m}x^{-\frac{5}{2}}-\frac{3a}{2m}x^{-\frac{7}{2}}\] \[\Rightarrow\omega=\sqrt{\frac{b}{2m}x^{-\frac{5}{2}}-\frac{3a}{2m}x^{-\frac{7}{2}}}=\sqrt{\frac{bx-3a}{2mx^{\frac{7}{2}}}}\] \[T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{2mx^{\frac{7}{2}}}{bx-3a}}\]6)
Над шоссе висит источник звуковых сигналов с частотой $\nu=2.3\ кГц$ . К нему со скоростью $v=54\ км/ч$ приближается мотоциклист, ветер дует противоположно его движению со скоростью $u=5\ м/с$. Считая скорость звука $v_0=340\ м/с$, найти частоту сигнала, воспринимаемую мотоциклистом.
高速公路上方悬挂着一个频率为 $\nu=2.3\ kHz$ 的声音信号源。 一个摩托车手以 $v=54\ km/h$ 的速度接近他,风以 $u=5\ m/s$ 的速度与他的运动相反。 假设声速$v_0=340\ m/s$,求摩托车手感知到的信号频率。
Решение
За время $t$ мотоциклист проедет путь $S=vt$.
За это время мотоциклист “услышит” все звуковые импульсы испущенные источником
т.е
\[N=\nu(t+\frac{S}{v_0+u})\]Следовательно, мотоциклист будет воспринимать сигнал частотой
\[f=\frac{N}{t}=\frac{\nu(t+\frac{S}{v_0+u})}{t}=\frac{\nu(t+\frac{vt}{v_0+u})}{t}=\nu(1+\frac{v}{v_0+u})=\nu(\frac{v_0+u+v}{v_0+u})=2300(\frac{345+15}{345})=2400Hz\]