MainPage/Probability Theory/HomeWork
Состав домашних заданий
Домашнее задание No1 (теория вероятностей) Вариант 24
- Рябушко Индивидуальные задания по высшей математике. В 4 ч. Ч.4 Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика: ИДЗ 18-1 (6 задач), ИДЗ 18-2 (4 задачи) по своему номеру в журнале.
- Курс теории вероятностей, Чистяков В.П. Главы 2-6 по 5 любых задач из каждой главы (всего 25 задач)
Срок сдачи – 8-9 неделя.
ИДЗ-18.1
1.24. Сколько перестановок можно сделать из букв слова «ракета», чтобы все они начинались с буквы «р»? (Ответ: 60.)
Первая всегда «р», переставляем только последние $5$ букв
Получается $A_5^5=5!=120$ вариантов.
Но у нас две буквы «р» одинаковы, поэтому на вариантов надо в $2$ раза меньше.
2.24. Мальчик забыл две последние цифры номера телефона одноклассника и набрал их наугад, помня только, что эти цифры нечетны и различны. Найти вероятность того, что номер набран правильно. (Ответ: 0,05.)
\[P=\frac{N}{\Omega}=\frac{1}{A_5^2}=\frac{1}{20}=0.05\]3.24. В ящике 50 % деталей, изготовленных на заводе №1, 20 % – на заводе №2 и 30 % – на заводе №3. Наугад взято три детали. Найти вероятность того, что:
\[\begin{cases} p_1=0.5\\ p_2=0.2\\ p_3=0.3\\ \end{cases}\]а) все три детали – с завода №1;
\[P=p_1^3=0.5^3=0.125\]б) две детали – с завода №1;
\[P=p_1^2p_2+p_1^2p_3=0.5\times 0.5\times 0.2 + 0.5\times 0.5\times 0.3 = 0.5^3 = 0.125\]в) все три детали – с разных заводов.
\[P=p_1p_2p_3=0.5\times 0.2\times 0.3 = 0.03\](Ответ: а) 0,125; б) 0,125; в) 0,03.)
4.24. В состав блока входит 6 радиоламп первого типа и 10 второго. Гарантийный срок обычно выдерживает 80 % радиоламп первого типа и 90 % второго типа. Найти вероятность того, что:
событие $A$ - «случайно выбранная радиолампа выдержит гарантийный срок»;
гипотеза $H_1$ - «выбранная радиолампа в блоке 1-ого типа»
гипотеза $H_2$ - «выбранная радиолампа в блоке 2-ого типа»
\[P(H_1)=\frac{6}{16}=0.375\] \[P(H_2)=\frac{10}{16}=0.625\] \[P(A\lvert H_1) = 0.8\] \[P(A\lvert H_2) = 0.9\]а) наугад взятая радиолампа выдержит гарантийный срок;
\[P=P(H_1)\times P(A\lvert H_1) + P(H_2)\times P(A\lvert H_2) = 0.8625\]б) радиолампа, выдержавшая гарантийный срок, первого типа.
\[P(H_1\lvert A)=\frac{P(H_1)P(A\lvert H_1)}{P(A)}=\frac{\frac{6}{15}\times 0.8}{\frac{6}{15}\times 0.8 + \frac{10}{16}\times0.9}=\frac{0.375\times0.8}{0.8625}=0.3478\](Ответ: а) 0,8625; б) 0,3478.)
5.24. Вероятность поражения цели каждым из семи выстрелов равна 0,8. Найти вероятность поражения цели:
\[n=7, p=0.8\]а) двумя выстрелами;
\[P(X=2)=C_7^2\times0.8^2\times0.2^5\approx0.0032\]б) хотя бы одним выстрелом;
\[P(X\ge 1)=1-P(X=0)=1-C_7^0\times0.8^0\times0.2^7\approx0.999987\]в) не менее чем тремя выстрелами.
\[P(X\ge3)=1-C_7^0\times0.8^0\times0.2^7-C_7^1\times0.8^1\times0.2^6-C_7^2\times0.8^2\times0.2^5=1-0.0000128-0.0003584-0.0043008\approx0.9953\](Ответ: а) 0,0043; б) 0,99998; в) 0,9953.)
6.24. Вероятность того, что изделие – высшего качества, равна 0,5. Найти вероятность того, что из 400 изделий число изделий высшего качества составит от 194 до 208. (Ответ: 0,5138.)
Формула теоремы Муавра-Лапласа:
\[P_n(k_1; k_2)\approx\Phi(\frac{k_2-np}{\sqrt{npq}})-\Phi(\frac{k_1-np}{\sqrt{npq}})\]где
\[\Phi(x)=\frac{2}{\sqrt{2\pi}}\int_0^xe^{-\frac{t^2}{2}} {\rm d}t\]У нас:
- $n=400$
- $k_1=194$
- $k_2=208$
- $p=q=0.5$
Поэтому
\[P_{400}(194;208)\approx\Phi(\frac{208-400\times0.5}{\sqrt{400\times0.5^2}})-\Phi(\frac{194-400\times0.5}{\sqrt{400\times0.5^2}})=\Phi(0.8)-\Phi(-0.6)\approx0.28814+0.22575=0.51389\]ИДЗ-18.2
1.24. Вероятности поражения цели каждым из трех стрелков равны соответственно 0,7; 0,8; 0,6; СВ Х – число поражений цели при условии, что каждый из стрелков сделал по одному выстрелу. (Ответ: M (X) = 2,1, D (X) = 0,61.)
\[p_1=0.7,p_2=0.8,p_3=0.6\] \[q_1=1-p_1=0.3,q_2=1-p_2=0.2,q_3=1-p_3=0.4\]при $X=0$
\[\widetilde{p_0}=q_1 q_2 q_3=0.024\]при $X=1$
\[\widetilde{p_1}=p_1 q_2 q_3+q_1 p_2 p_3+q_1 q_2 p_3=0.188\]при $X=2$
\[\widetilde{p_2}=p_1 p_2 q_3+p_1 q_2 p_3+q_1 p_2 p_3=0.452\]при $X=3$
\[\widetilde{p_3}=p_1p_2p_3=0.336\]| $x_1$ | 0 | 1 | 2 | 3 | sum |
|---|---|---|---|---|---|
| $\widetilde{p_i}$ | 0.024 | 0.188 | 0.452 | 0.336 | 1 |
| $x_1\widetilde{p_i}$ | 0 | 0.188 | 0.904 | 1.008 | 2.1 |
| $x_i^2\widetilde{p_i}$ | 0 | 0.188 | 1.808 | 3.024 | 5.02 |
2.24.
\[F(x)=\begin{cases} 0\quad при\ x\lt 0\\ \frac{1}{6}x\quad при\ 0\le x\le 6\\ 1\quad при\ x\gt 6\\ \end{cases}\](Ответ: $M(x) = 3, D(x) = 3, P(2≤x≤5) = 0,5$.)
\[f(x)=F'(x)=\begin{cases} 0\quad при\ x\lt 0\\ \frac{1}{6}\quad при\ 0\le x\le 6\\ 1\quad при\ x\gt 6\\ \end{cases}\] \[\begin{split} M(x)&=\int_{-\infty}^\infty xf(x) {\rm d}x\\ &=\int_0^6\frac{1}{6}x {\rm d}x\\ &=\frac{1}{6}\int_0^6x {\rm d}x\\ &=\frac{1}{6}\cdot\frac{1}{2}x^2\Big\rvert_0^6\\ &=\frac{1}{6}\times18=3 \end{split}\] \[\begin{split} D(x)&=\int_{-\infty}^\infty x^2f(x) {\rm d}x-M(x)^2\\ &=\int_0^6\frac{1}{6}x^2 {\rm d}x-3^2\\ &=\frac{1}{6}\int_0^6x^2 {\rm d}x-9\\ &=\frac{1}{6}\cdot\frac{1}{3}x^3\Big\rvert_0^6-9\\ &=12-9=3 \end{split}\] \[P(2\le X\le5)=F(5)-F(2)=\frac{5}{6}-\frac{2}{6}=\frac{1}{2}\]3.24. Найти дисперсию и среднее квадратичное отклонение СВ Х, распределенной равномерно в интервале (2; 10). (Ответ: D(X) = 5,33 , σ(X) = 2,31 .)
равномерное распределение
\[f(x)=\begin{cases} 0\qquad при\ x\lt a\ или\ x\gt b\\ \frac{1}{b-a}\qquad при\ a\le x\le b\\ \end{cases}\] \[M(x)=\frac{a+b}{2}\] \[M(x)=\frac{(b-a)^2}{12}\]У нас $a=2,b=10$, Поэтому:
\[M(x)=\frac{2+10}{2}=6\] \[D(x)=\frac{(10-2)^2}{12}=\frac{8^2}{12}=\frac{64}{12}\approx5.33\] \[\sigma(x)=\sqrt{D(x)}\approx\sqrt{5.33}\approx2.31\]4.24. Среднее значение скорости ветра у земли в данном пункте равно 16 м/ч. Оценить вероятность того, что в этом пункте скорость ветра не будет превышать 80 м/ч. (Ответ: не менее 0,8.)
Неравенство Маркова
\[P(X\ge A)\le\frac{M(X)}{A}\]У нас $A=80, M(X)=16$, Поэтому:
\[P(X\ge80)\le\frac{M(X)}{80}=\frac{16}{80}=\frac{1}{5}\] \[P(X\le80)\ge1-\frac{1}{5}=\frac{4}{5}=0.8\]Домашнее задание No2 (Математическая статистика) Вариант 24
Рябушко Индивидуальные задания по высшей математике. В 4 ч. Ч.4 Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика ИДЗ-19.1, ИДЗ-19.2 Вариант тот же: номер в журнале. Срок сдачи – 14-15 неделя.
ИДЗ-19.1
| 76 | 28 | 151 | 91 | 60 | 204 | 177 | 102 | 128 | 217 |
| 120 | 66 | 207 | 126 | 124 | 152 | 27 | 221 | 131 | 51 |
| 241 | 77 | 250 | 134 | 123 | 147 | 184 | 195 | 47 | 160 |
| 159 | 74 | 169 | 178 | 79 | 129 | 250 | 223 | 182 | 96 |
| 135 | 199 | 56 | 25 | 82 | 116 | 44 | 229 | 145 | 203 |
| 88 | 209 | 146 | 224 | 239 | 103 | 201 | 245 | 130 | 163 |
| 71 | 165 | 176 | 194 | 78 | 154 | 99 | 78 | 127 | 69 |
| 171 | 173 | 31 | 181 | 117 | 84 | 73 | 161 | 240 | 149 |
| 247 | 107 | 140 | 53 | 205 | 155 | 29 | 132 | 185 | 179 |
| 180 | 128 | 42 | 114 | 93 | 191 | 174 | 210 | 133 | 226 |
В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:
-
а) записать значения результатов эксперимента в виде вариационного ряда;
25 27 28 29 31 42 44 47 51 53 56 60 66 69 71 73 74 76 77 78 78 79 82 84 88 91 93 96 99 102 103 107 114 116 117 120 123 124 126 127 128 128 129 130 131 132 133 134 135 140 145 146 147 149 151 152 154 155 159 160 161 163 165 169 171 173 174 176 177 178 179 180 181 182 184 185 191 194 195 199 201 203 204 205 207 209 210 217 221 223 224 226 229 239 240 241 245 247 250 250 -
б) найти размах варьирования и разбить его на 9 интервалов;
- размах варьирования: $\omega = x_{max}-x_{min}=250-25=225$
-
разбить на 9 интервалов:
По фориуле $h=\omega / l$, где $l$ – число интервалов
вычисляем длину частичного интервала $h=225/9=25$Номер частичноuо интервала $l_i$ Границы интервала $x_i-x_{i+1}$ Середина интервала $x’i=(x_i+x{i+1})/2$ Частота интервала $n_i$ Относительная частота $W_i=n_i/n$ Плотность относительной частоты $W_i/h$ 1 [25-50) 37.5 8 0.08 0.0032 2 [50-75) 62.5 9 0.09 0.0036 3 [75-100) 87.5 12 0.12 0.0048 4 [100-125) 112.5 9 0.09 0.0036 5 [125-150) 137.5 16 0.16 0.0064 6 [150-175) 162.5 13 0.13 0.0052 7 [175-200) 187.5 13 0.13 0.0052 8 [200-225) 212.5 11 0.11 0.0044 9 [225-250] 237.5 9 0.09 0.0036 $\sum_i$ - - 100 1 -
-
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
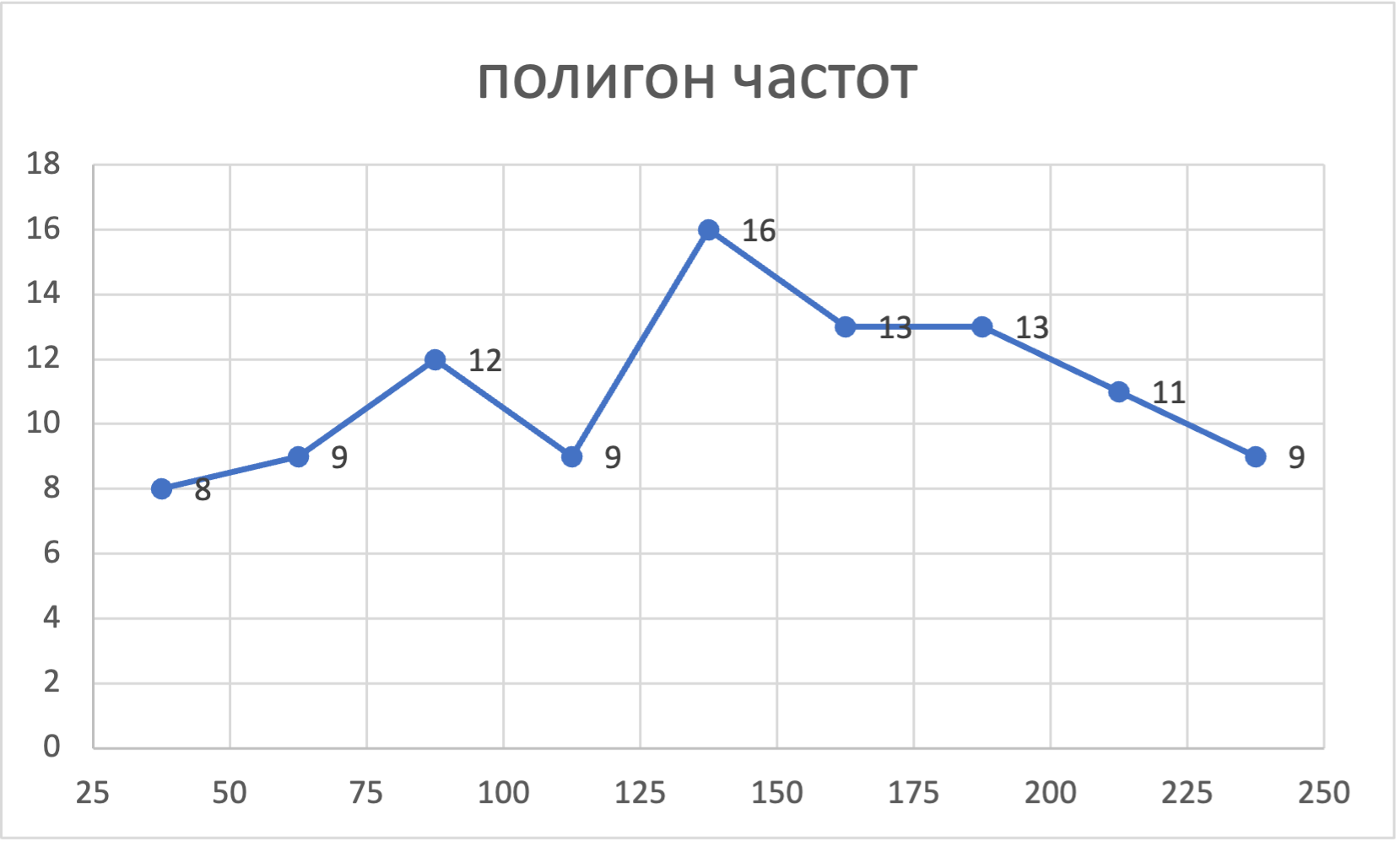
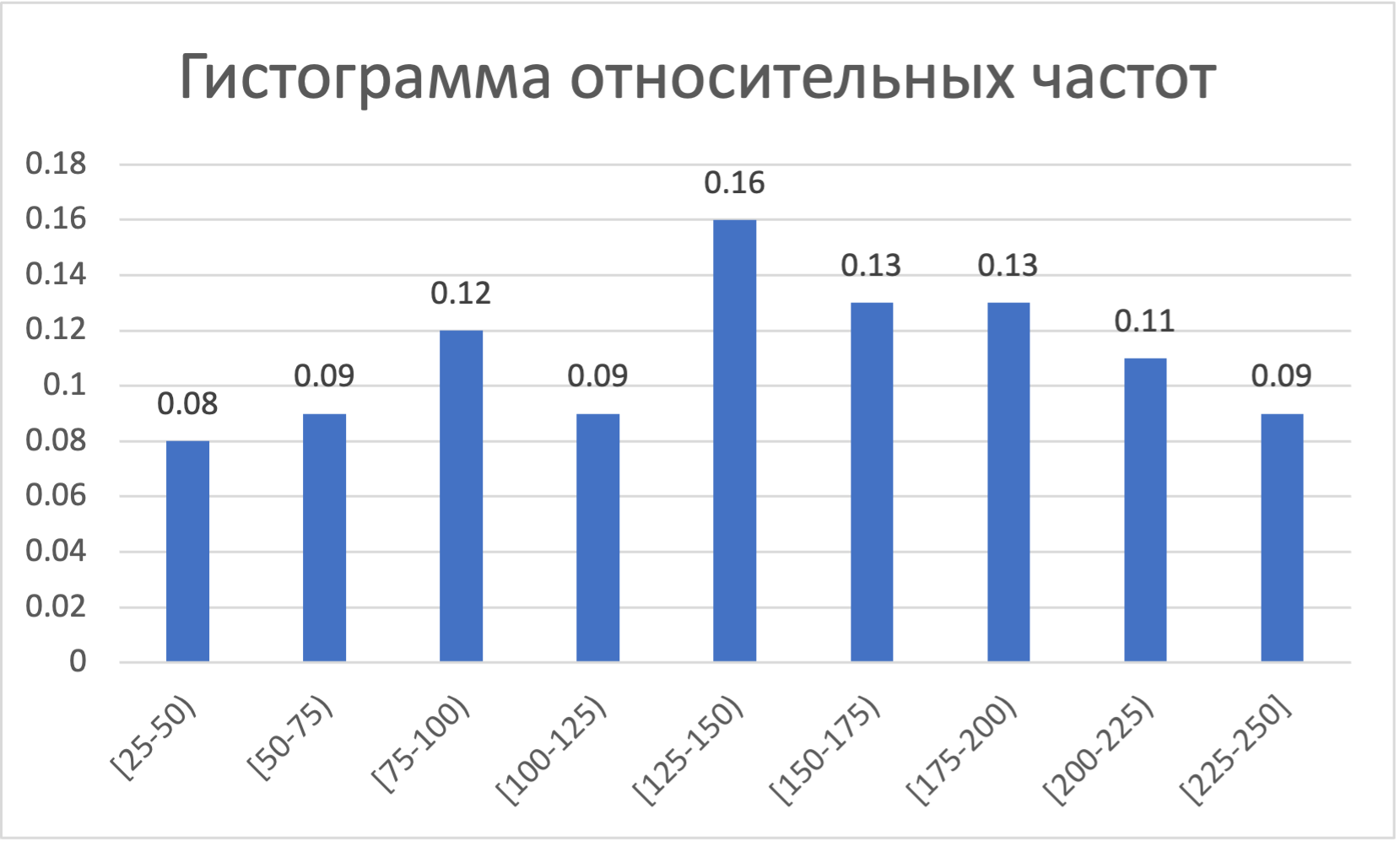
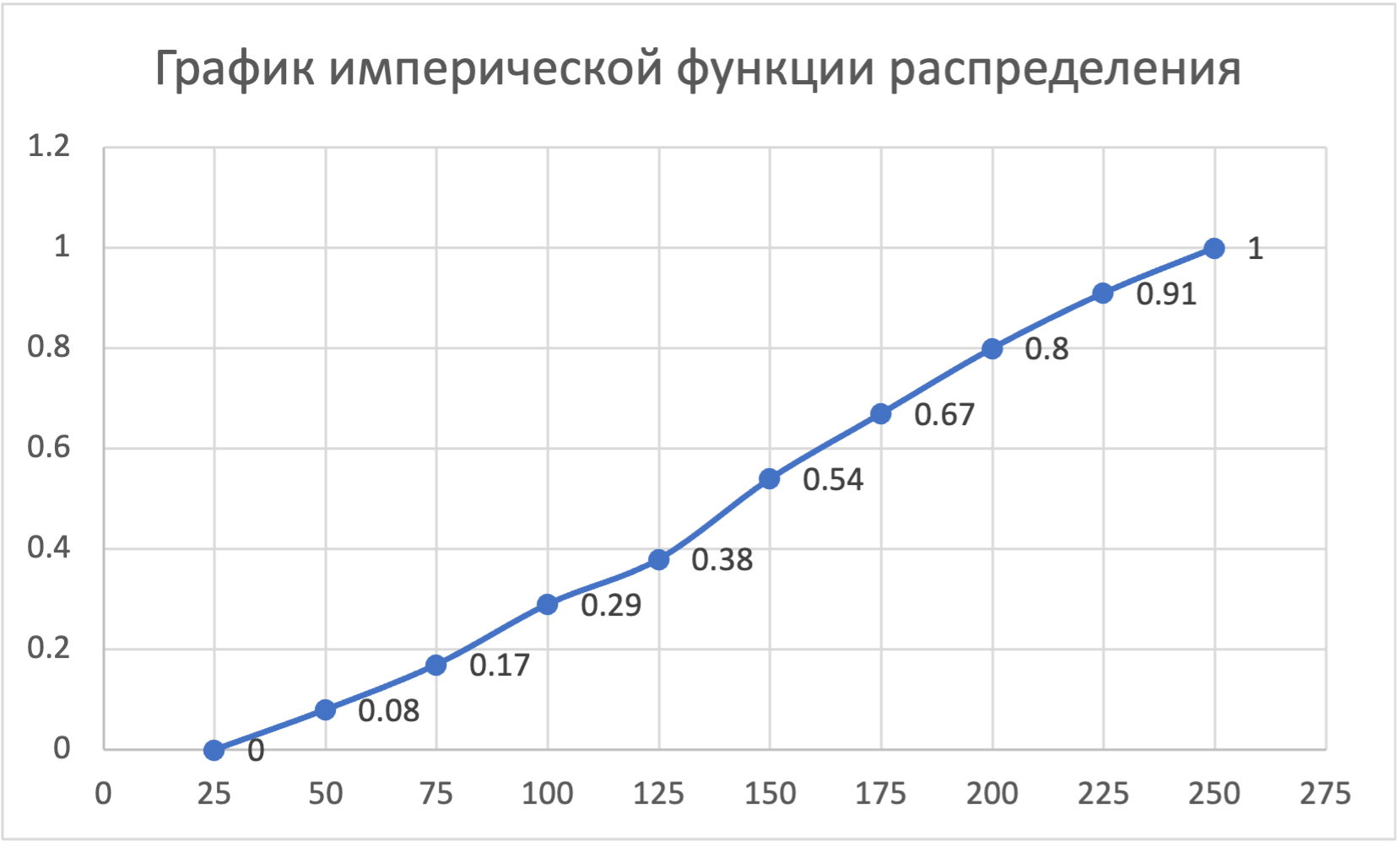
-
г) найти числовые характеристики выборки $\overline{x}$, $D_B$;
| m_i | Границы интервала $ x_i; x_{i+1}$ | Середина интервала $x’_i$ | Частота интервала $n_i$ | $n_ix’_i$ | $(x’_i)^2$ | $n_i(x’_i)^2$ | |—|—|—|—|—|—|—| | 1 | [25-50) | 37.5 | 8 | 300 | 1406.25 | 11250 | | 2 | [50-75) | 62.5 | 9 | 562.5 | 3906.25 | 35156.25| | 3 | [75-100) | 87.5 | 12| 1050 | 7656.25 | 91875 | | 4 | [100-125)| 112.5 | 9 | 1012.5| 12656.25 | 113906.25 | | 5 | [125-150)| 137.5 | 16| 2200 | 18906.25 | 302500 | | 6 | [150-175)| 162.5 | 13| 2112.5| 26406.25 | 343281.25 | | 7 | [175-200)| 187.5 | 13| 2437.5| 35156.25 | 457031.25 | | 8 | [200-225)| 212.5 | 11| 2337.5| 45156.25 | 496718.75 | | 9 | [225-250]| 237.5 | 9 | 2137.5| 56406.25 | 507656.25 | | $\sum_i$ | | |100| 14150 | 207656.25 | 2359375 |- $\overline{x}=\frac{1}{n}\sum_{i=1}^kx’_i\cdot n_i=141.5$
- $D_B=\frac{1}{n}\sum_{i=1}^k(x’_i)^2n_i-\overline{x}^2=23593.75-20022.25=3571.25$
- $\sigma_B=\sqrt{D_B}\approx59.7599$
- $\widetilde{D}_B=\frac{n}{n-1}\cdot D_B\approx3607.32$
- $\widetilde{\sigma_B}=\sqrt{\widetilde{D}_B}\approx60.06$
-
д) приняв в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости $\alpha = 0.025$;
$i$ $x_i$ $x_{i+1}$ $x_i-\overline{x}$ $x_{i+1}+\overline{x}$ $z_i=(x_i-\overline{x})/\sigma_B$ $z_{i+1}=(x_{i+1}-\overline{x})/\sigma_B$ 1 25 50 - -91.5 - -1.53 2 50 75 -91.5 -66.5 -1.53 -1.11 3 75 100 -66.5 -41.5 -1.11 -0.69 4 100 125 -41.5 -16.5 -0.69 -0.28 5 125 150 -16.5 8.5 -0.28 0.14 6 150 175 8.5 33.5 0.14 0.56 7 175 200 33.5 58.5 0.56 0.98 8 200 225 58.5 83.5 0.98 1.40 9 225 250 83.5 - 1.40 - i $z_i$ $z_{i+1}$ $\Phi(z_i)$ $\Phi(z_{i+1})$ $P_i=\Phi(z_{i+1}-\Phi(z_i))$ $n_i=100\cdot P_i$ 1 - -1.53 -0.5 -0.437 0.063 6.3 2 -1.53 -1.11 -0.437 -0.3438 0.0932 9.32 3 -1.11 -0.69 -0.3438 -0.2549 0.0889 8.89 4 -0.69 -0.28 -0.2549 -0.1103 0.1446 14.46 5 -0.28 0.14 -0.1103 0.0557 0.166 16.6 6 0.14 0.56 0.0557 0.2123 0.1566 15.66 7 0.56 0.98 0.2123 0.3365 0.1242 12.42 8 0.98 1.40 0.3365 0.4192 0.0827 8.27 9 1.40 - 0.4192 0.5 0.0808 8.08 $\sum_i$ 1 100 $i$ $n_i$ $n’_i$ $n_i-n’_i$ $(n_i-n’_i)^2$ $\frac{(n_i-n’_i)^2}{n’_i}$ $n_i^2$ $\frac{n_i^2}{n’_i}$ 1 8 6.3 1.7 2.89 0.458730159 64 10.15873016 2 9 9.32 -0.32 0.1024 0.010987124 81 8.690987124 3 12 8.89 3.11 9.6721 1.087975253 144 16.19797525 4 9 14.46 -5.46 29.8116 2.061659751 81 5.601659751 5 16 16.6 -0.6 0.36 0.021686747 256 15.42168675 6 13 15.66 -2.66 7.0756 0.451826309 169 10.79182631 7 13 12.42 0.58 0.3364 0.027085346 169 13.60708535 8 11 8.27 2.73 7.4529 0.901197098 121 14.6311971 9 9 8.08 0.92 0.8464 0.104752475 81 10.02475248 $\sum_i$ 100 100 5.125900263 105.1259003 - $\chi_{набл}^2=\frac{1}{n}\sum_{i=1}^kn_i^2-n\approx5.1259$
- Контроль: $105.1259-100=5.1259$
- $k=l-3=9-3=6$
- $\chi_{кр}^2=14.4$ при $\alpha = 0.025$, и при количестве степеней свободы: $k=6$
- Так как $\chi_{кр}^2\gt \chi_{набл}^2$, то гипотеза принимается.
-
е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности $\gamma = 0.9$.
-
Математическое ожидание покрывается доверительным интервалом:
\[(\overline{x}-\frac{\widetilde{\sigma_B}}{\sqrt{n}}t_\gamma;\overline{x}+\frac{\widetilde{\sigma_B}}{\sqrt{n}}t_\gamma)\]Так как $\gamma = 0,9$, то $t_\gamma = 1.65$, при $\overline{x} = 141.5$, $\widetilde{\sigma_B}=60.06$, $n=100$
Тогда доверительный интервал: $(131.59;151.41)$ -
Доверительный интервал для среднеквадратичного отклонения находится по формуле:
\[(\widetilde{\sigma_B}(1-q);\widetilde{\sigma_B}(1+q))\]$q=0.143$ при $n = 100$ и $\gamma = 0.95$
Тогда доверительный интервал: $(51.47;68.65)$
-
ИДЗ-19.2
| $X/Y$ | 1470 | 1540 | 1610 | 1680 | 1750 | 1820 | 1890 | 1960 | $m_x$ |
|---|---|---|---|---|---|---|---|---|---|
| 210 | 3 | 2 | 3 | – | – | – | – | – | 8 |
| 220 | - | 1 | 4 | 5 | - | - | - | - | 10 |
| 230 | - | - | 7 | 13 | 8 | - | - | - | 28 |
| 240 | - | - | - | - | 9 | 6 | 6 | - | 21 |
| 250 | - | - | - | - | - | 7 | 8 | 3 | 18 |
| 260 | - | - | - | - | - | 4 | 6 | 5 | 15 |
| $m_y$ | 5 | 5 | 12 | 22 | 20 | 12 | 11 | 13 | 100 |
Дана таблица распределения 100 заводов по производственным средствам $X$ (тыс. ден. ед.) и по суточной выработке $Y$ (т). Известно, что между $X$ и $Y$ существует линейная корреляционная зависимость. Требуется:
-
а) найти уравнение прямой регрессии $y$ на $x$;
- j 1 2 3 4 5 6 7 8 9 10 11 12 13 i $X/Y$ 1470 1540 1610 1680 1750 1820 1890 1960 $m_{x_i}$ $m_{x_i}x_i$ $\sum_{j=1}^km_{y_j}y_j$ $x_i^2m_{x_i}$ $x_i\sum_{j=1}^km_{ij}y_j$ 1 210 3 2 3 0 0 0 0 0 8 1680 12320 352800 2587200 2 220 0 1 4 5 0 0 0 0 10 2200 16380 484000 3603600 3 230 0 0 7 13 8 0 0 0 28 6440 47110 1481200 10835300 4 240 0 0 0 0 9 6 6 0 21 5040 38010 1209600 9122400 5 250 0 0 0 0 0 7 8 3 18 4500 33740 1125000 8435000 6 260 0 0 0 0 0 4 6 5 15 3900 28420 1014000 7389200 7 $m_{y_j}$ 3 3 14 18 17 17 20 8 100 23760 175980 5666600 41972700 8 $m_{y_j}y_j$ 4410 4620 22540 30240 29750 30940 37800 15680 175980 9 $\sum_{i=1}^mm_{ij}x_i$ 630 640 3120 4090 4000 4230 5000 2050 23760 10 $y_j^2m_{ij}$ 6482700 7114800 36289400 50803200 52062500 56310800 71442000 30732800 311238200 11 $y_j\sum_{i=1}^mm_{ij}x_i$ 926100 985600 5023200 6871200 7000000 7698600 9450000 4018000 41972700 При построении таблицы надо выполнить проверку:
$\sum_{i=1}^6m_{xi}=\sum_{j=1}^8m_{yj}=n=100$
$\sum_{i=1}^6\sum_{j=1}^8m_{ij}x_i=\sum_{i=1}^6m_{xi}x_i=23760$
$\sum_{i=1}^6\sum_{j=1}^8m_{ij}y_j=\sum_{j=1}m_{y_j}y_j=175980$
$\sum_{i=1}^6(x_i\sum_{j=1}^8m_{ij}y_j)=\sum_{j=1}^8(y_j\sum_{i=1}^6m_{ij}x_i)=41972700$
$\overline{x}=\frac{\sum\sum m_{ij}x_i}{n}=\frac{\sum m_{x_i}x_i}{n}=\frac{23760}{100}=237.6$
$\overline{y}=\frac{\sum m_{y_j}y_j}{n}=\frac{175980}{100}=1759.8$
$s_x^2=\frac{1}{n-1}(\sum m_{x_i}x_i^2-\frac{1}{n}(\sum m_{x_i}x_i)^2)=\frac{1}{99}(5666600-\frac{1}{100}23760^2)\approx214.38$
$s_y^2=\frac{1}{n-1}(\sum m_{y_j}y_j^2-\frac{1}{n}(\sum m_{y_j}y_j)^2)=\frac{1}{99}(311238200-\frac{1}{100}175980^2)\approx15642.38$
$s_{xy}=\frac{1}{n-1}(\sum\sum m_{ij}x_iy_j-\frac{1}{n}(\sum m_{x_i}x_i)(\sum m_{y_j}y_j))=\frac{1}{99}(41972700-\frac{1}{100}(23760\cdot175980))\approx1614.67$
Оценкой теоретической линии регрессии является эмпи- рическая линия регрессии,уравнение которой имеет вид
\[y=\overline{y} + r_{xy}\frac{s_y}{s_x}(x-\overline{x})\]где $s_x=\sqrt{214.38}\approx14.64$; $s_y=\sqrt{15642.38}\approx125.07$
$r_{xy}=\frac{s_{xy}}{s_xs_y}=\frac{1614.67}{14.64\cdot125.07}\approx0.88$
Составляем уравнение эмпирической линии регрессии $y$ на $x$:
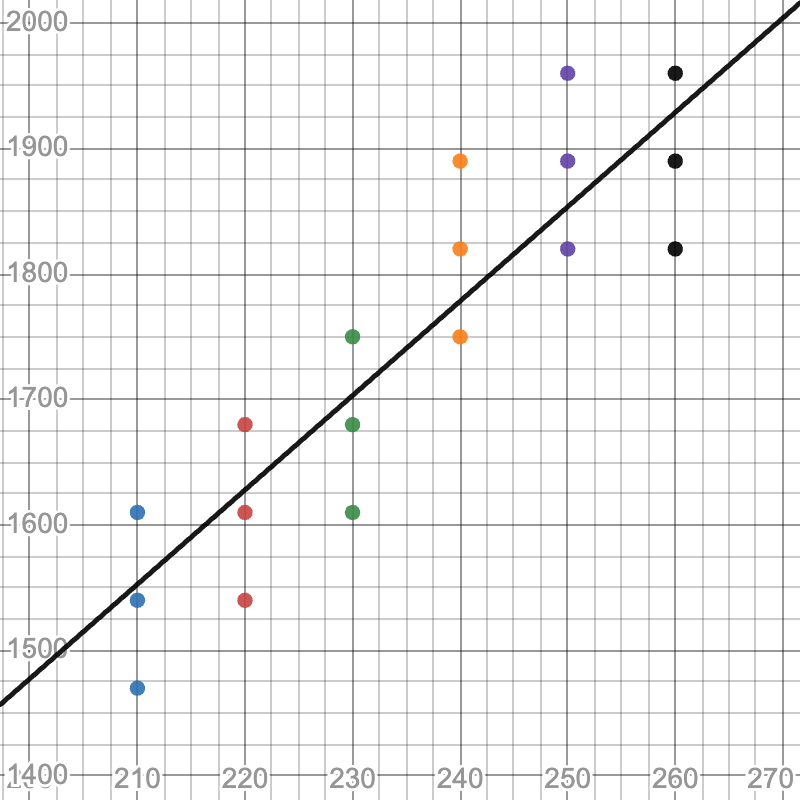
\[y=1759.8+0.88\frac{125.07}{14.64}(x-237.6)\Rightarrow y=7.52x-26.45\] -
б) построить уравнение эмпирической линии регрессии и случайные точки выборки $(X, Y)$.