MainPage/Probability Theory/Lecture

• MainPage/Probability Theory/Lecture
• Лекция 1
  • Основные понятия и определения
  • Основные понятия и определения
  • Основные понятия и определения
  • Основные понятия и определения
  • Строгие определения
  • Свойства операций над событиями
  • Вероятность. Аксиомы теории вероятностей.
  • Основные теоремы и следствия теории вероятностей
  • Основные теоремы и следствия теории вероятностей
  • Основные теоремы и следствия теории вероятностей
  • Классическая схема вычисления вероятностей
  • Декартово произведение множеств и правило умножения
  • Декартово произведение множеств и правило умножения
  • Правило умножения и правило сложения
  • Размещения и перестановки
  • Размещения с повторениями
  • Сочетания
  • Сочетания с повторениями
  • Перестановки с повторениями
  • Геометрическая схема вычисления вероятности
  • Условная вероятность
  • Вероятность произведения двух событий
  • Независимость событий
  • Независимость системы событий
  • Формула полной вероятности
  • Формула полной вероятности
  • Формула Байеса
• Лекция 2 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
  • Независимые испытания. Схема Бернулли.
  • Формула Бернулли.
  • Полиномиальное распределение
  • Теорема Пуассона
  • Математическая модель простейшего потока событий
  • Локальная теорема Муавра-Лапласа
  • Функция Гаусса
  • Интегральная теорема Муавра-Лаплоса
  • Нормированная функция Лапласа
  • Функция Лапласа
  • Случайная величина
  • Строгое определение
  • Многоугольник (полигон) распределения
  • Дискретная случайная величина
  • Дискретная случайная величина
  • Функция распределения случайной величины
  • Свойства функции распределения
  • Непрерывная случайная величина
  • Функция распределения дискретной случайной величины
  • Плотность распределения вероятностей
  • Свойства плотности распределения
• Лекция 3 Числовые характеристики случайных величин
  • Числовые характеристики случайных величин
  • Математическое ожидание дискретной случайной величины
  • Вероятностный смысл математического ожидания
  • Математическое ожидание дискретной случайной величины
  • Математическое ожидание непрерывной случайной величины
  • Свойства математического ожидания
  • Дисперсия случайной величины
  • Дисперсия случайной величины
  • Свойства дисперсии
  • Свойства дисперсии
  • Среднее квадратическое отклонение
  • Стандартная случайная величина
  • Моменты случайной величины
  • Центральный момент
  • Производящая функция
  • Производящая функция
  • Биноминальный закон распределения
• Распределение Пуассона
• Геометрическое распределение
• Лекция 4

Лекция 1

Основные понятия и определения

Теория вероятностей — это математическая дисциплина, в рамках которой моделируют и изучают такие события в повседневной жизни, науке и технике, которые носят случайный характер.

В теории вероятностей первичным понятием является произвольное множество. Элементы $\omega$ этого множества называют элементарными событиями, а само множество $\Omega$ называют пространством элементарных событий.

Для описания каждой реальной задачи пространство $\Omega$ выбирается наиболее подходящим образом. Пусть, например, опыт состоит в подбрасывании один раз правильной шестигранной игральной кости. Наблюдаемый результат — число очков на верхней грани. Пространство элементарных событий $\Omega$ в этом случае равно множеству ${1, 2, 3, 4, 5, 6}$, а элементарные события — цифры от одной до шести.

Пространство $\Omega$ может быть дискретным или непрерывным. Дискретные пространства подразделяются на конечные и счетные — эквивалентные множеству натуральных чисел.

Если пространство $\Omega$ дискретно, то случайным событием может быть любое подмножество пространства элементарных событий. События обозначают прописными буквами латинского алфавита: $A, B, C, …, Z$ . Говорят, что событие A произошло (наступило, реализовалось), если результатом опыта явился элементарный исход, принадлежащий $A$.

Основные понятия и определения

Событие, совпадающее с пустым множеством $\varnothing$ , называется невозможным событием, а событие, совпадающее со всем множеством $\Omega$, — достоверным событием. Невозможное событие не происходит ни в одном опыте, а достоверное — осуществляется всегда.

Если пространство $\Omega$ непрерывно, то событиями являются не любые его подмножества, а только те, которые принадлежат $\sigma$ - алгебре событий, т. е. семейству подмножеств, замкнутому относительно основных операций над множествами. Для того, чтобы задать $\sigma$ - алгебру событий, надо предварительно определить основные операции и отношения между событиями. Поскольку любое событие отождествляется с некоторым множеством, то над событиями можно совершать те же операции, что и над множествами.

Множества, состоящие из одинаковых элементов, называют равными.

Если каждый элемент множества $A$ является также элементом множества $B$ , то пишут $A \subset B$ и говорят, что $A$ есть подмножество $B$ или $A$ включено в $B$ или $A$ внутри $B$ .

Основные понятия и определения

С помощью логических символов определение включения одного множества в другое записывается следующим образом:

\[A \subset B \Leftrightarrow \forall x(x \in A \rightarrow x \in B) \Leftrightarrow (x \in A \Rightarrow x \in B).\]

Если $A$ и $B$ — события и $A \subset B$ , то говорят, что из события $A$ следует событие $B$ . Иначе говоря, событие B происходит всякий раз, как происходит событие $A$ . В примере с игральной костью из события «число выпавших очков будет кратно 5 » следует событие «число выпавших очков будет нечетно», так как ${5} \subset {1, 3, 5}$.

Суммой двух событий $A$ и $B$ называется событие $A + B$, являющееся объедине- нием $A \cup B$. Событие $A + B$ состоит в том, что произошло по крайней мере одно из событий A или B.

Произведением событий $A$ и $B$ называется событие AB, равное пересечению $A \cap B$. Событие $AB$ происходит тогда и только тогда, когда происходит и $A$ и $B$.

Если множества не имеют общих элементов, то их называют непересекающимися, а соответствующие события –– несовместными. Для двух множеств $A$ и $B$ в этом случае $AB = \varnothing$ . Например, события «выпадет чётное число очков» и «выпадет нечётное число очков» несовместны, так как множества $A = {2, 4, 6}$ и $B = {1, 3, 5}$ не пересекаются.

Основные понятия и определения

События $A_1, A_2,… , A_n$ образуют полную группу, если они попарно несовместны, а в сумме дают достоверное событие. Например, указанные выше события $A = {2, 4, 6}$ и $B = {1, 3, 5}$ образуют полную группу.

Разностью двух множеств $A$ и $B$ называют множество $A \setminus B$ , состоящее из тех элементов, которые входят в $A$ , но не входят в $B$ :

\[A \setminus B = \{x \in \Omega |x \in A \cap x ƒ\in B\}\]

Разности множеств соответствует разность событий. Это новое событие, состоящее в том, что A происходит, а B не происходит. Например, если $A = {1, 2, 3, 4}$ — множество очков меньших пяти, $B = {2, 4, 6}$ — множество чётных очков, то $A \ B = {1, 3}$. Если рассматривается разность между пространством элементарных событий и некоторым множеством $A$ , то разность $\Omega \setminus A$ называется дополнением множества $A$ и обозначается $\overline{A}$ . Событие $\overline{A}$ называют событием противоположным $A$ . Это событие,состоящее в том, что $A$ не происходит. Так, событием противоположным событию $A = {1, 2, 3, 4}$ будет событие выпадение числа очков больших или равных пяти .

Строгие определения

Определение $\sigma$ -алгебры. Семейство подмножеств $S$ пространства $\Omega $ называют $\sigma$ -алгеброй, если выполняются следующие условия:

• пустое множество $\varnothing$ и само пространство $\Omega $ входят в $S$ ;
• данное семейство замкнуто относительно теоретико- множественных операций, включая счетные объединения и пересечения множеств из $S$ .

Определение события.

Событием называют некоторое подмножество пространства элемен- тарных событий $\Omega $ , принадлежащее $\sigma$ - алгебре пространства $\Omega $ .

Свойства операций над событиями

Операции над событиями обладают следующими свойствами:

• $A+B = B+A\ A\cdot B = B\cdot A$ (переместительное)
• $(A+B)\cdot C = A\cdot C + B\cdot C, A\cdot B + C=(A+C)\cdot(B+C)$ (распределительное)
• $(A+B)+C=A+(B+C), (A\cdot B)\cdot C=A\cdot(B\cdot C)$ (сочетательное)
• $A+A=A, A\cdot A = A$
• $A+\Omega = \Omega, A\cdot \Omega=A$
• $A+\overline{A}=\Omega, A\cdot\overline{A}=\varnothing$
• $\overline{\varnothing}=\Omega,\overline{\Omega}=\varnothing,\overline{\overline{A}}=A$
• $A-B=A\cdot\overline{B}$
• $\overline{A+B}=\overline{A}\cdot\overline{B}, \overline{A\cdot B}=\overline{A}+\overline{B}$ (закон Де Моргана)

Вероятность. Аксиомы теории вероятностей.

Вероятностью называется числовая функция $P : F \rightarrow R$, заданная на $\sigma$-алгебре событий $F$ , которая должна удовлетворять трем аксиомам: 1) $P(A) \ge 0$ для любого $A \in F$ (неотрицательность $P$); 2) $P(\Omega ) = 1$ (нормированность $P$); 3) $P(A + B) = P(A) + P(B)$ для любых $A, B \in F , AB = \varnothing$ (аддитивность $P$): для несовместных событий вероятность суммы событий равна сумме их вероятностей.

Тройку ${\Omega , S, P }$, где $S$ есть $\sigma$ -алгебра подмножеств пространства элементарных событий $\Omega $ , $P$ — числовая функция, удовлетворяющая трем аксиомам, называют вероятностным пространством случайного опыта, а неотрицательную, нормированную и аддитивную вероятностную функцию $P (A), A \in S, A \subset \Omega $ — распределением вероятностей.

Аксиоматическая теория вероятностей в ее современном виде была создана русским математиком А. Н. Колмогоровым в 1933 году.

Основные теоремы и следствия теории вероятностей

Теорема (о монотонности распределения вероятностей).

Если из события $A$ следует событие $B$ , то справедлива формула:

\[P (A) \le P (B)\]

Доказательство. Так как $A \subset B$ , то событие B представимо в виде

\[B = B\Omega = B(A +\overline{A}) = BA + B\overline{A}= A + B\overline{A}\]

Отсюда, используя аксиому сложения, получим $P (B) = P (A) + P (B\overline{A})$ . Так как в силу аксиомы 1 справедливо неравенство $P (B\overline{A}) \ge 0$ , то из предшествующего равенства следует доказательство теоремы.

Основные теоремы и следствия теории вероятностей

Теорема (о вероятности противоположного события).

Вероятность противоположного события вычисляется по формуле:

\[P (\overline{A}) = 1 − P (A)\]

Доказательство. Из равенства $A + A ^- = \Omega $ и аксиомы сложения следует $P (A) + P (A^-) = P (\Omega )$ . В силу аксиомы нормированности $P (\Omega ) = 1$ , так что из предшествующего равенства получаем доказываемую формулу.

Отсюда, учитывая, что невозможное и достоверное события взаимно противоположны, т. е. справедливо равенство $\varnothing + \Omega = \Omega $ , выводится утвер- ждение $P (\varnothing) = 0$: «вероятность невозможного события равна нулю».

Для любого события $A$ истинны соотношения $\varnothing \subset A \subset \Omega $. Отсюда, учитывая монотонность распределения вероятностей, следуют неравенства $0 \le P (A) \le 1$ , утверждающие, что вероятность любого события всегда лежит между нулем и единицей.

Основные теоремы и следствия теории вероятностей

Теорема (о вероятности суммы совместных событий).

Для любых двух событий верна формула сложения вероятностей:

\[P (A \cup B) = P (A) + P (B) − P (AB)\]

Доказательство. Представим событие $A \cup B$ в виде $A \cup B = A + B\overline{A}$, а событие $B$ в виде $B = B\overline{A}+BA$ . События в правых частях данных равенств несовместны, поэтому по аксиоме сложения получим:

\[P(A\cup B)=P(A)+P(B\overline{A}), P(B)=P(B\overline{A})+P(BA)\]

Отсюда следует доказываемая формула сложения вероятностей. Из формулы сложения вероятностей по индукции выводится общая формула вероятности суммы любого конечного числа событий. В частности, формула вычисления вероятности суммы трех событий имеет вид

\[P (A \cup B \cup C) = P (A) + P (B) + P (C) − P (AB) − P (AC) − P (BC) + P (ABC)\]

Классическая схема вычисления вероятностей

Пусть пространство элементарных событий $\Omega$ конечно, состоит из $n$ равновероятных исходов, вероятность каждого исхода равна $1/n$ и, следовательно, сумма вероятностей всех исходов равна единице. Определим вероятность каждого события $A \subset \Omega $ как сумму вероятностей тех исходов, которые входят в это подмножество. Все аксиомы теории вероятностей выполняются при такой схеме задания вероятностей событий, и, соответственно, выполняются все выводы, которые следуют из аксиом. Данную конечную схему вычисления вероятностей называют классической, а вероятность любого события $A \subset \Omega $ находят по формуле классической вероятности:

\[P(A)=\frac{N(A)}{N(\Omega)}\]

где буквой $N$ обозначено число элементов в множестве.

Таким образом, вероятность любого случайного события в классической схеме равна отношению числа исходов, благоприятствующих появлению этого события, к общему числу элементарных исходов.

При решении многих задач с использованием классической схемы часто оказываются полезными различные комбинаторные формулы.

Декартово произведение множеств и правило умножения

Пусть заданы два множества $A$ и $B$ с произвольным числом элементов любой природы в каждом множестве. Образуем новое множество по правилу: $D = {(a, b)

a \in A, b \in B}$. Это новое множество называется прямым или декартовым произведением множеств $A$ и $B$ и обозначается $D = A \times B$ . Элементы прямого произведения представляют собой упорядоченные пары, причём две упорядоченные пары равны только в том случае, когда у них равны первые элементы и равны вторые элементы.

Пример. Имея множества $A = {1; 2}$ и $B = {\alpha; \beta}$ , можно образовать декартовы произведения следующего вида:

\[D_1=A\times B=\{(1,\alpha);(1,\beta); (2,\alpha);(2,\beta)\}\] \[D_1=A\times B=\{(\alpha,1);(\alpha,2); (\beta,1);(\beta,2)\}\]

Как видно из примера, декартово произведение не обладает свойством коммутативности. Свойство коммутативности выполняется только для равных между собой множеств.

Декартово произведение множеств и правило умножения

Если дана система множеств $A_1, A_2,… , A_n$ , то элементами декартова произведения являются упорядоченные наборы ($a_1, a_2,… , a_n$) , т. е.:

\[A_1 \times A_2 \times ··· \times A_n = {(a_1, a_2, ... , a_n)|a_1 \in A_1, a_2 \in A_2, ..., a_n \in A_n}\]

В том случае, когда сомножители декартова произведения являются конечными множествами, можно непосредственно подсчитать, что число упорядоченных наборов ($a_1, a_2, …, a_n$) в декартовом произведении равно произведению чисел элементов в каждом из множеств, т. е. справедлива формула:

\[N (A_1 \times A_2 \times ··· \times A_n) = N (A_1) · N (A_2)\quad N(A_n)\]

Данная формула является основной в комбинаторном анализе и обычно называется принципом или правилом умножения.

В частности, в рассмотренном ранее примере исходных множеств всего два и каждое содержит по два элемента, так что в декартовом произведении содержится четыре элемента.

Правило умножения и правило сложения

Правило умножения. Если из некоторого конечного множества первый элемент $a_1$ можно выбрать $n_1$ способами, а второй элемент $a_2$ можно выбрать $n_2$ способами, то оба элемента $(a_1, a_2)$ в указанном порядке можно выбрать $n_1 · n_2$ способами.

Правило сложения. Если из некоторого конечного множества первый элемент $a_1$ можно выбрать $n_1$ способами, а второй элемент $a_2$ можно выбрать $n_2$ способами, то хотя бы один из этих элементов ($a_1$ или $a_2$) можно выбрать $n_1 + n_2$ способами.

Правила умножения и сложения справедливы для любого конечного числа (два и более) выбираемых элементов.

Размещения и перестановки

Пусть имеется некоторое множество из $n$ элементов. Каждое его упорядоченное подмножество, состоящее из $k$ элементов, называется размещением из $n$ элементов по $k$ . Согласно определению, одно размещение отличается от другого либо составом элементов, либо их порядком.

Число размещений находится по правилу умножения в виде

\[A_n^k=n\cdot(n-1)\cdot(n-2)\cdot...\cdot(n-k+1)\]

или

\[A_n^k=\frac{n!}{(n-k)!}\]

В частном случае $k = n$ размещения называют перестановками. Одна перестановка отличается от другой только порядком расположения элементов, а число всевозможных перестановок в конечном множестве из $n$ элементов вычисляется по следующей формуле:

\[P_n=A_n^n=n!\]

Размещения с повторениями

Пусть некоторый опыт состоит в случайном выборе $k$ элементов из множества, содержащего n элементов. Выбор организован таким образом, что каждый выбранный элемент возвращается обратно, так что при следующем выборе может быть взят как новый элемент, так и прежний. В дальнейшем отобранные элементы упорядочиваются либо в порядке поступления, либо по указанному в решаемой задаче правилу. Полученное таким образом соединение называют размещением с повторениями. Одно размещение с повторениями может отличаться от другого элементами, их порядком и количеством повторений элементов. Число всех размещений из $n$ элементов по $k$ с повторениями обозначается $\overline{A_n^k}$ и находится по следующей формуле:

\[\overline{A_n^k}=n^k\]

При выводе данной формулы использовался комбинаторный принцип умножения $k$ множеств, каждое из которых содержит $n$ элементов.

Сочетания

Любое подмножество из $k$ элементов некоторого множества из $n$ элементов называют сочетанием из $n$ по $k$ . Одно сочетание отличается от другого хотя бы одним элементом. Число сочетаний находят по формулам:

\[C_n^k=\frac{A_n^k}{k!}=\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}=\frac{n!}{k!(n-k)!}\]

Действительно, любое подмножество, содержащее $k$ элементов множества из $n$ элементов, может быть упорядочено $k!$ способами. Таким образом, общее число размещений $A_n^k$ больше общего числа соответствующих сочетаний $C_n^k$ в $k!$ раз, т. е.

\[A_n^k=k!\cdot C_n^k\]

Разделив формулы для числа размещений на $k!$, получим формулу вычисления количества сочетаний.

Для чисел $C_n^k$ , называемых также биномиальными коэффициентами, справедливы следующие тождества:

$C_n^k=C_n^{n-k}$ - (свойство симметрии), $C_{n+1}=C_n^k+C_n^{k-1}$ - (рекуррентное соотношение), $C_n^0+C_n^1+C_n^2+\cdots+C_n^n=2^n$ - (следствие биномиальной формулы Ньютона).

Сочетания с повторениями

В данной схеме случайный выбор $k$ элементов из множества, содержащего $n$ элементов, организован таким образом, что каждый выбранный элемент возвращается обратно, так что при каждом следующем выборе может быть взят как новый элемент, так и любой ранее выбранный. Полученное таким образом соединение называют сочетанием с повторениями. Одно сочетание с повторениями отличается от другого хотя бы одним элементом или числом повторений элемента. Число всех сочетаний с повторениями из $n$ элементов по $k$ обозначается $\overline{C_n^k}$ и находится по следующей формуле:

\[\overline{C_n^k}=C_{c+k-1}^k\]

Действительно, в соответствии со схемой с возвращением и упорядочиванием, используя правило умножения, получим, что число упорядоченных соединений длиной $k$ равно $n(n + 1)(n + 2) \cdots (n + k − 1)$ . Разделив данное число на k! и домножив числитель и знаменатель полученной дроби на $(n − 1)!$ , найдем число сочетаний с повторениями в указанном выше виде

\[\overline{C_n^k}=\frac{(n-1)!\cdot n(n+1)(n+2)\cdots(n+k-1)}{k!\cdot(n-1)!}=\frac{(n+k-1)!}{k!\cdot(n-1)!}=C_{n+k-1}^k\]

Перестановки с повторениями

В схеме упорядоченных разбиений множество, содержащее n элементов, разбивается на k упорядоченных подмножеств так, что первое подмножество содержит $n_1$ элементов первого типа, второе — $n_2$ элементов второго типа и т. д., а последнее — $n_k$ элементов $k$ -того типа, причем $n_1 + n_2 + \cdots + n_k = n$. Каждое такое разбиение образует соединение из $n$ элементов, которое называют перестановкой с повторениями. Число всех перестановок с повторениями называется полиноминальным коэффициентом, обозначается $P_n(n_1, n_2, \cdots , n_k)$ и вычисляется по следующей формуле:

\[P_n(n_1, n_2, \cdots , n_k)=\frac{n!}{n_1!\cdot n_2!\cdot...\cdot n_k!}\]

Действительно, в соответствии со схемой разбиения множества на упорядоченную конечную систему подмножеств и, используя правило умножения, получим, что число таких соединений длиной $n$ находится с помощью следующих преобразований:

\[P_n(n_1, n_2, \cdots, n_k)=C_n^{n_1}\cdot C_{n-n_1}^{n_2}\cdot C_{n-n_1-n_2}^{n_3}\cdot...\cdot C_{n_k}^{n_k}\\ =\frac{n!}{n_1!(n-n_1)!}\cdot\frac{(n-1)!}{n_2!(n-n_1-n_2)!}\cdot...\cdot\frac{n_k!}{0!\cdot n_k!}=\frac{n!}{n_1!\cdot n_2\cdot...\cdot n_k!}\]

Геометрическая схема вычисления вероятности

Формула классической вероятности следующим образом обобщается на случай непрерывных пространств элементарных исходов. Рассмотрим в качестве $\sigma$ -алгебры $S$ систему измеримых подмножеств пространства $\Omega$ . Пусть условия опыта таковы, что вероятность попадания в произвольное измеримое подмножество пропорциональна мере этого подмножества и не зависит от его местоположения в пространстве $\Omega$ . Данный опыт можно интерпретировать как бросание случайной точки на пространство $\Omega$. При этих условиях вероятность появления любого события $A$ из $S$ вычисляется по так называемой формуле геометрической вероятности:

\[P(A)=\frac{\mu(A)}{\mu(\Omega)}\]

где буквой $\mu$ обозначена мера множества (длина, площадь или объем ).

Геометрическая вероятность события $A$ из $S$ удовлетворяет всем аксиомам теории вероятностей, что позволяет применять к ней утверждения и теоремы, доказанные в рамках аксиоматики Колмогорова.

Условная вероятность

Пусть $A$ и $B$ - два события, рассматриваемые в данном оппыте. Наступление одоного события (скажем, $A$) может влиять на вощможность наступления другого ($B$). Для характеристики зависимости одних событий от других вводится понятие условной вероятность.

Условной вероятностью события $B$ при условии реализации события $A$ называется отношение вероятности произведения событий $A$ и $B$ к вероятности события $A$, т.е.

\[P_A(B)=\frac{P(AB)}{P(A)}, P(A)\ne0\]

Другие обозначение:

\[P(B\lvert A)=\frac{P(A\cdot B)}{P(A)}\]

Вероятность $P(B)$, в отличие от условной, называется безусловной вероятность.

Вероятность произведения двух событий

Вероятность произведения двух событий равна произведению безусловной вероятности одного из них на условную вероятность другого, при условии, что первое событие произошло:

\[P(AB)=P(A)\cdot P_A(B)=P(B)\cdot P_B(A);P(A)>0, P(B)>0\]

Доказательство. Данные формулы непосредственно следуют из определения условной вероятности.

Применяя правило умножения индуктивно получают формулу умножения вероятностей для системы событий в следующем виде:

\[P(A_1A_2\cdots A_n)=P(A_1)\cdot P_{A_1}(A_2)\cdot P_{A_1A_2}(A_3)\cdots P_{A_1A_2\cdots A_n-1}(A_n)\]

Независимость событий

События $A$ и $B$ называются независимыми, если вероятность произведения данных событий равна произведению их вероятностей:

\[P(AB)=P(A)\cdot P(B)\]

Для двух независимых событий условная вероятность каждого из событий равна безусловной вероятности, что вытекает из следующих соотношений:

\[P_A(B)=\frac{P(AB)}{P(A)}=\frac{P(A)\cdot P(B)}{P(A)}=P(B),P(A)\ne0\] \[P_B(A)=\frac{P(AB)}{P(B)}=\frac{P(A)\cdot P(B)}{P(B)}=P(A),P(B)\ne0\]

Таким образом, для независимых событий появление одного из событий никак не влияет на вероятность появления другого. Иногда именно равенство $PA(B) = P (B)$ берут за исходное определение независимости события $B$ от события $A$ . Однако, мы будем использовать более симметричное определение независимости, рассмотренное А.Н. Колмогоровым.

Пример. Проводится опыт, состоящий в двукратном подбрасывании симметричной монеты. В этом случае пространство элементарных событий состоит из четырех исходов: $\Omega = { ГГ, ГР, РГ, РР }$. Рассмотрим событие $A = { ГГ, ГР }$ «выпадение «герба» при первом подбрасывании монеты» и событие $B = { ГГ, РГ }$ — «выпадение «герба» при втором подбрасывании». Тогда произведение событий $AB = { ГГ }$ — выпадение герба при первом и втором подбрасывании монеты. По классической схеме вычисления вероятностей $P(A)=P(B)=1/2, P(AB)=1/4$. События $A$ и $B$ независимы, поскольку выполняется условие $P (AB) = P (A) \cdot P (B)$.

Для двух независимых событий формула вероятности произведения событий имеет вид:

\[P(AB)=P(A)\cdot P(B)\]

Независимость системы событий

Система из n событий называется независимой, если для любой ее подсистемы из $k \le n$ событий справедливы следующие формулы :

\[P(A_1A_2\cdots A_k)=P(A_1)\cdot P(A_2)\cdot ...\cdot P(A_k)\]

Из независимости системы событий непосредственно из опре- деления следует попарная независимость событий. Обратное утверждение неверно

Для системы из n независимых событий формула вероятности произведения событий выводится по индукции и имеет вид:

\[P(A_1A_2\cdots A_n)=P(A_1)\cdot P(A_2)\cdot ...\cdot P(A_n)\]

Формула полной вероятности

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса. Напомним, что события $A_1, A_2, …, A_n$ образуют полную группу, если $A_i\cdot A_j=\varnothing, i\ne j, \sum_{i=1}^nA_i=\Omega$. Систему таких событий называют также разбиением.

Теорема. Пусть события $H_1, H_2, …, H_n$. образуют полную группу. Тогда для любого, наблюдаемого в опыте, события А имеет место формула полной вероятности.

\[P(A)=\sum_{i=1}^nP(H_i)\cdot P(A\lvert H_i)\]

Формула полной вероятности

Доказательство: Так как $H_1+H_2+… +H_n = \Omega$, то в силу свойств операций над событиями

\[A = A \cdot \Omega = A \cdot (H_1 + H_2 + ... + H_n) =A \cdot H_1 + A \cdot H_2 + ... + A\cdot H_n\]

Из того, что $H_i\cdot H_j=\varnothing$, следует, что $(A\cdot H_i)\cdot(A\cdot H_j)=\varnothing, i\ne j$ т. е. события $A\cdot H_i$ и $A\cdot H_j$ также несовместны. Тогда по тео]>еме сложения вероятностей $P(A) = P(A\cdot H_1) + P(A \cdot Н_2) + … + P(A\cdot H_n)$ т.е. $P(A) = \sum_{i=1}^n P(A\cdot H_i)$. По теореме умножения вероятностей $P(A \cdot H_i)=P(H_i)\cdot P(A\lvert H_i)$, откуда и следует формула полной вероятности.

В формуле полной вероятности события $H_1, H_2, …, H_n$ обычно называют гипотезами} они исчерпывают все возможные предположения (гипотезы) относительно исходов как бы первого этапа опыта, событие $A$ — один из возможных исходов второго этапа.

Формула Байеса

Следствием формулы полной вероятности является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез $H_i$, принятых до опыта и называемых априорными («а priori», доопытные, лат.) по результатам уже проведенного опыта, т. е. найти условные вероятности $P(H_i\lvert A)$, которые называют апостериорными («а posteriori», послеопытные).

Теорема. Пусть события $H_1, H_2, …, H_n$ образуют полную группу событий. Тогда условная вероятность события $H_k(k = 1,n)$ при условии, что событие $A$ произошло, задается формулой

\[P(H_k\lvert A)=\frac{P(H_k)\cdot P(A\lvert H_k)}{P(A)}\]

где $P(A) = P(H_1)\cdot P(A\lvert H_1)+ … + P(H_n)\cdot P(A\lvert H_n)$ — формула полной вероятности

Доказательство: Применив формулы условной вероятности и умножения вероятностей, имеем

\[P(H_k\lvert A)=\frac{P(H_k\cdot A)}{P(A)}=\frac{P(H_k)\cdot P(A\lvert H_k)}{P(A)}\]

где $P(A)$ — формула полной вероятности

Лекция 2 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Независимые испытания. Схема Бернулли.

С понятием «независимых событий» связано понятие «независи­ мых испытаний (опытов)».

Несколько опытов называются независимыми, если их исходы представляют собой независимые события (независимые в совокупно­ сти).

Последовательность $n$ независимых испытаний, в каждом из кото­рых может произойти некоторое событие $A$ (его называют успехом) с вероятностью $P(A) = p$ или противоположное ему событие $A$ (его на­ зывают неудачей) с вероятностью $P(\overline{A}) = q = 1 - p)$, называется схемой Бернулли.

Например, при стрельбе по мишени: событие $A$ попадание (успех), событие $\overline{A}$ — промах (неудача); при обследовании п изделий на предмет годности: событие $A$ — деталь годная (успех), событие $A$ деталь бракованная (неудача) и т. д.

В каждом таком опыте ПЭС состоит только из двух элементар­ ных событий, т. е. $\Omega = {\omega_0,\omega_1}$, где $\omega_0$ — неудача, $\omega_1$ успех, при этом $A = {\omega_1}, \overline{A} — {\omega_0}$. Вероятности этих событий обозначают че­ рез р и q соответственно ($p + q = 1$). Множество элементарных исхо­ дов для п опытов состоит из $2^n$ элементов. Например, прп $n = 3$, т. е. опыт повторяется 3 раза, $\Omega=\big{\frac{\overline{A},\overline{A},\overline{A}}{\omega_0};\frac{A,A,\overline{A}}{\omega_1};\frac{\overline{A},A,\overline{A}}{\omega_2};\frac{\overline{A},A,A}{\omega_3};\frac{A,\overline{A},\overline{A}}{\omega_4};\frac{A,\overline{A},A}{\omega_5};\frac{\overline{A},\overline{A},A}{\omega_6};\frac{A,A,A}{\omega_7}$. Вероятность каждого элемен­тарного события определяется однозначно. По теореме умножения ве­роятность события, скажем $\omega_6=(\overline{A},\overline{A},A)$, равна $q\cdot q\cdot p=pq^2$, события $\omega_7 - p\cdot p\cdot p=p^3q^0$ и т. д.

Часто успеху сопоставляют число 1, неудаче — число 0. Элемен­ тарным событием для п опытов будет последовательность из п нулей и единиц. Тройка чисел $(0,0,0)$ означает, что во всех трех опытах со­бытие А не наступило; тройка чисел $(0,1,0)$ означает, что событие $A$ наступило во 2-м опыте, а в 1-м и 3-м — не наступило.

Формула Бернулли.

Простейшая задача, относящаяся к схеме Бернулли, состоит в определении вероятности того, что в п независимых испытаниях собы­тие $A$ наступит $m$ раз ($0\le m\le n$). Обозначается искомая вероятность так: $P_n(m)$ или $P_{n,m}$ или $P(\mu_n=m)$, где $\mu_n$ — число появления события $A$ в серии из $n$ опытов.

Например, при бросании игральной кости 3 раза $P_3(2)$ означает вероятность того, что в 3-х опытах событие $А$ — выпадение цифры 4 произойдет 2 раза. Очевидно,

\[P_3(2)=p^2q+p^2q+p^2q=\Big[\{(A,A,\overline{A});(A,\overline{A},A);(\overline{A},A,A)\}\Big]=3p^2q=3\cdot(\frac{1}{6})^2\cdot\frac{5}{6}=\frac{5}{72}=0.069\]

Теорема Если производится $n$ независимых испытаний, в каждом из которых вероятность появления события $A$ равна $p$, а вероятность его непоявления равна $q = 1 — p$, то вероятность того, что событие $A$ произойдет т раз определяется формулой Бернулли

\[P_n(m)=C_n^m\cdot p^m\cdot q^{n-m}, m=0,1,2,\cdots,n\]

Доказательство: Вероятность одного сложного события, состоящего в том, что со­бытие $A$ в $n$ независимых опытах появится т раз в первых т опы­тах и не появится $(n-m)$ раз в остальных опытах (это событие $\underbrace{A\cdot A\cdot A\cdot A\cdot … \cdot A}{m\ раз}\cdot\underbrace{\overline{A}\cdot \overline{A}\cdot \overline{A}\cdot \overline{A}\cdot … \cdot \overline{A}}{(n-m)\ раз}$ по теореме умножения вероятностей равна $p^mq^{n-m}$. Вероятность появления события А снова т раз, но в другом порядке (например, $\overline{A}\cdot\underbrace{A\cdot A\cdot …\cdot A}_{m\ раз}\overline{A}\cdot\overline{A}\cdot …\cdot\overline{A}$ или $A\overline{A}A\overline{A}\cdot…\cdot A\overline{A}$ и т. д.) будет той же самой, т. е. $p^mq^{n-m}$

Число таких сложных событий — в $n$ опытах т раз встречается со­ бытие А в различном порядке — равно числу сочетаний из п по т. е. $C_n^m$. Так как все эти сложные события несовместны, то по теореме сло­ жения вероятностей искомая вероятностъ равна сумме вероятностей всех возможных сложных событий, т. е.

\[P_n(m)=\underbrace{p^mq^{n-m}+\cdots+p^mq^{n-m}}_{C_n^m слагаеиых}=C_n^mp^mq^{n-m}\quad m=0,1,\cdots,n\]

Можно заметить, что вероятности $P_n(m), m=0,1,\cdots, n$ являются коэффициентами при хт в разложении $(q+px)^n$ по формуле бинома Ньютона:

\[(q+px)^n=q^n+C^1_nq^{n-1}px+C_n^2q^{n-2}p^2x^2+\cdots+C_n^mq^{n-m}p^mx^m+\cdots+p^nx^n\]

Поэтому совокупность вероятностей $P_n(m)$ называют биномиальным законом распределения вероятностен (см. п. 2.7), а функцию $\varphi(x)=(q+px)^n$ — производящей функцией для последовательности неза­висимых опытов.

Полиномиальное распределение

Если в каждом из независимых испытаний вероятности наступле­ ния события $A$ разные, то вероятность того, что событие $A$ наступит $m$ раз в $n$ опытах, равна коэффициенту при $m$-й степени многочлена $\varphi_n(z)=(q_1+p_1z)(q_2+p^2z)\cdot…\cdot(q_n+p^nz)$, где $\varphi_n(z)$ — производящая функция.

Если в серии из $n$ независимых опытов, в каждом из которых может произойти одно и только одно из $k$ событий $A_1,A-2,\cdots A_k$ соответ­ствующими вероятностями $p_1,p_2,\cdots p_k$ то вероятность того, что в этих опытах событие $A_1$ появится $M_1$ раз, событие $A_2 - m_2$ раз, $…$ событие $A_k - m_k$ раз, равна

\[P_n(m_1,m_2,\cdots m_k)=\frac{n!}{m_1!m_2!\cdots m_k!}p_1^{m_1}p_2^P{m_2}\cdots p_k^{m_k}\]

где $m_1+m_2+\cdots+m_k=n$. Вероятности (1.33) называются полиноми­ альным распределением.

Теорема Пуассона

Теорема Если число испытаний неограничено увеличивается $(n\to \infty)$ и вертятность $p$ наступления события $A$ в каждом испытании неограничено уменьшается $(p \to 0)$, но так, что их произведение $np$ является постоянной величиной ($np = a = const$), то вероятность $P_n(m)$ удовлетворяет предельному равенству

\[\lim_{n\to\infty}P_n(m)=\frac{a^m e^{-a}}{m!}\]

Это выражение называется ассимптотической формулой Пуассона.

Доказательство:

Преобразуем формулу Бернулли с учетом того, что $p=\frac{a}{n}$:

\[\begin{split} P_n(m)=\frac{n!}{m!(n-m)!}\cdot(\frac{a}{n})^m\cdot(1-\frac{a}{n}^{n-m})=\\ \frac{n(n-1)(n-2)\cdots(n-(m-1))}{m!}\cdot\frac{a^m}{n^m}\cdot(1-\frac{a}{n})^n\cdot(1-\frac{a}{n})^{-m}\\ =\frac{a^m}{m!}\cdot\frac{n}{n}\cdot\frac{n-1}{n}\cdot\frac{n-2}{n}\cdot...\cdot\frac{n-(m-1)}{n}\cdot(1-\frac{a}{n})^n\cdot(1-\frac{a}{n})^{-m}\\ =\frac{a^m}{m!}\cdot1\cdot(1-\frac{1}{n})\cdot(1-\frac{2}{n})\cdot...\cdot(1-\frac{m-1}{n})\cdot(1-\frac{a}{n})^n\cdot(1-\frac{a}{n})^{-m}\\ \end{split}\]

Переходя к пределу при $n\to \infty$, получим $\lim_{n\to\infty}P_n(m)=\frac{a^me^{-a}}{m!}$ ($\lim_{n\to\infty}(1-\frac{a}{n})^n=e^{-a}$ согласно второму замечательному пределу)

Из предельного равенства теоремы Пуассона при больших $n$ и малых $p$ вытекает приближенная формула Пуассона:

\[P_n(m)\approx\frac{a^me^{-a}}{m!}, a=np, m=0,1,2\cdots\]

Формула применяется, когда вероятность успеха крайне мала, т. е. сам по себе успех является редким событием. Её обычно используют, когда $n\ge 50$ а $np \le 10$

Формула Пуассона находит применение в теории массового обслуживания.

Математическая модель простейшего потока событий

Формулу Пуассона можно считать математической моделью про­стейшего потока событий.

Потоком событий называют последовательность событий, насту­ пающих в случайные моменты времени (например, поток посетителей в парикмахерской, поток вызовов на телефонной станции, поток отказов элементов, поток обслуженных абонентов и т.п.).

Поток событий, обладающий свойствами стационарности, ординар­ ности и отсутствия последствия называется простейшим (пуассоновским) потоком.

Свойство стационарности означает, что вероятность появления к событий на участке времени длины $\tau$ зависит только от его длины (т. е. не зависит от начала его отсчета). Следовательно, среднее число событий, появляющихся в единицу времени, так называемая интен­ сивность $\lambda$ потока, есть величина постоянная: $\lambda(t)=\lambda$.

Свойство ординарности означает, что событие появляется не груп­ пами, а поодиночке. Другими словами, вероятность появления более одного события на малый участок времени $\Delta t$ пренебрежительно мала по сравнению с вероятностью появления только одного события (на­пример, поток катеров, подходящих к причалу, ординарен).

Свойство отсутствия последствия означает, что вероятность по­ явления $k$ событий на любом участке времени длины $\tau$ не зависит от того, сколько событий появилось на любом другом не пересекающимся с ним участком (говорят: «будущее» потока не зависит от «прошлого», например, поток людей, входящих в супермаркет).

Можно доказать, что вероятность появления $m$ событий простей­ шего потока за время продолжительностью $t$ определяется формулой Пуассона

\[P_t(m)=p_m=\frac{(\lambda t)^m\cdot e^{-\lambda t}}{m!}\]

В тех случаях, когда число испытаний $n$ велико, а вероятность $p$ не близка к нулю ($p\ne 0 p\ne 1$), для вычисления биномиальных вероятностей используют теоремы Муавра-Лапласа. Приведем только их формулировки в силу сложности доказательства.

Локальная теорема Муавра-Лапласа

Теорема Локальная теорема Муавра-Лапласа Если вероят- ность р наступления события $A$ в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико, то вероятность $P_n(m)$ может быть вычислена по приближенной формуле

\[P_n(m)\approx\frac{1}{\sqrt{npq}}\cdot\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]

где $x=\frac{m-np}{\sqrt{npq}}$

Равенство тем точнее, чем больше $n$.

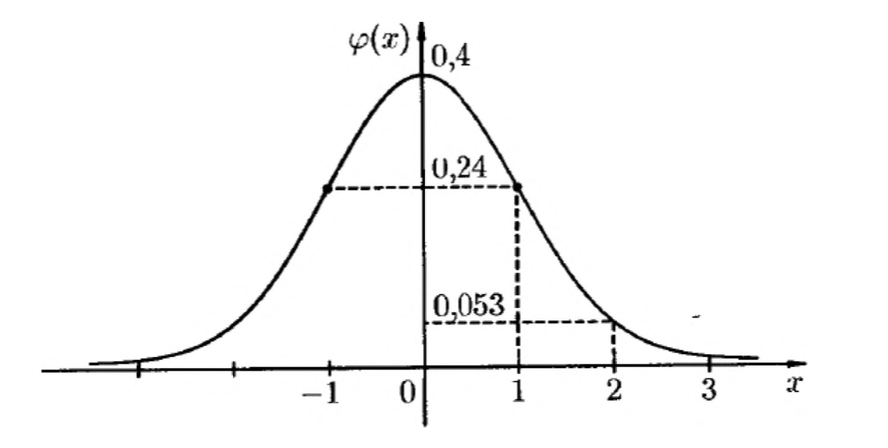
Функция Гаусса

Выражение

\[\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}=\varphi(x)\]

называется функцией Гаусса, а ее график — кривой вероятностей

Интегральная теорема Муавра-Лаплоса

В тех случаях, когда требуется вычислить вероятность того, что в п независимых испытаниях событие $A$ появится не менее $k_1$ раз, но не более $k_2$ раз, т. е. $P_n(k_1\le m\le k_2)$ или $P_n(k_1;k_2)$, используют инте­ гральную теорему Муавра—Лапласа (является частным случаем более общей теоремы — центральной предельной теоремы).

Теорема (Интегральная теорема Муавра-Лапласа) Если ве­ роятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность $P_n(k_1\le m\le k_2)$ может быть найдена по приближенной формуле

\[P_n(k_1\le m\le k_2)\approx\frac{1}{\sqrt{2\pi}}\int_{x_1}^{x_2}e^{-\frac{x^2}{2}}{ \rm d} x\]

где

• $x_1=\frac{k_1-np}{\sqrt{npq}}$
• $x_2=\frac{k_2-np}{\sqrt{npq}}$

Равенство тем точнее, чем больше $n$.

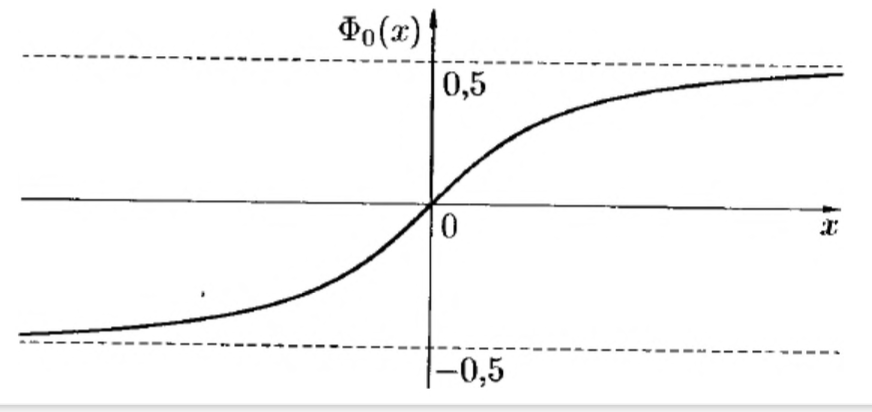
Нормированная функция Лапласа

для упрощения вычислений, вводят специальную функцию

\[\Phi_0(x)=\frac{1}{2\pi}\int_0^xe^{-\frac{t^2}{2}}{ \rm d}t\]

называемую нормированной функцией Лапласа.

Функция Лапласа

Наряду с нормированной функцией Лапласа используют функцию

\[\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{t^2}{2}}{ \rm d}t\]

называемую также функцией Лапласа. Для нее справедливо равенство $\Phi(-x)+\Phi(x)=1$; она связана с функцией $\Phi_0(x)$ формулой

\[\Phi(x)=0.5+\Phi_0(x)\]

Приближенную формулу для вычисления вероятности $P_n(k_1\le m\le k_2)$ можно записать в виде

\[P_n(k_1\le m\le k_2) = \Phi(x_2)-\Phi(x_1)=\Phi(x_2)-\Phi(x_1)\]

Где

• $x_1=\frac{k_1-np}{\sqrt{npq}}$
• $x_2=\frac{k_2-np}{\sqrt{npq}}$

Случайная величина

Под случайной величиной понимаю! величину, которая в результатк опыта принимает то или иное значение, причем неизвестно заранее, какое именно.

Примерами с. в. могут служить: 1) $X$ число очковч появляющихся при бросании игральной кости; 2) $Y$ — число выстрелов до первого попадания в цель; 3) $Z$ — время безотказной работы прибора и т.п.

(рост человека, курс доллара, количество бракованных деталей в пар­тии, температура воздуха, выигрыш игрока, координата точки при слу­чайном выборе ее на $[0; 1]$, прибыль фирмы, …).

Случайная величина, принимающая конечное или счетное множе­ ство значений, называется дискретной (сокращенно: д. с. в.).

Если же множество возможных значений с. в. несчетно, то такая величина называется непрерывной (сокращенно: н.с. в.).

Строгое определение

Случайной величиной $X$ называется числовая функция, опреде­ ленная на пространстве элементарных событий $\Omega$, которая каждому элементарному событию w ставит в соответствие число $X(\Omega)$, т.е.

\[X=X(\omega), \omega\in\Omega (или\ X=f(\omega))\]

Пример. Опыт состоит в бросании монеты 2 раза. На ПЭС $\Omega={\omega_1,\omega_2,\omega_3,\omega_4}$, где $\omega_1=ГГ, \omega_2=ГР, \omega_3=РГ, \omega_4=РР$, можно рассмотреть с. в. $X$ — число появлений герба. С. в. $X$ является функ­ цией от элементарного события $\omega_i$: $X(\omega_1)=2, X(\omega_2)=1, X(\omega_3)=1,X(\omega_4)=0$; $X$ - д. с. в. со значениями $x_1=0,x_2=1,x_3=2$.

Отметим, что если множество 12 конечно или счетно, то случай­ ной величиной является любая функция, определенная на $\Omega$. В общем случае функция $X (\omega)$ должна быть такова, чтобы для любых $x\in R$ событие $A={\omega: X(\omega) < x}$ принадлежало $\sigma$-алгебре множеств $S$ и, значит, для любого такого события была определена вероятность $P(A)=P(X<x)$

Закон распределения случайной величины

Для полного описания с. в. недостаточно лишь знания ее возмож­ ных значений; необходимо еще знать вероятности этих значений.

Любое правило (таблица, функция, график), позволяющее нахо­ дить вероятности произвольных событий $A\subseteq S$ ($S$ — $\sigma$-алгебра собы­тий пространства $\Omega$). в частности, указывающее вероятности отдель­ ных значений случайной величины или множества этих значений, на­зывается законом распределения случайной величины (или просто: рас­пределением). Про с. в. говорят, что «она подчиняется данному закону распределения»:

Пусть $Х$ — д.с.в., которая принимает значения $x_1,x_2,x_3,\cdots,x_n,\cdots$ (множество этих значений конечно или счетно) с некоторой вероят­ностью $p_i$ где $i = 1,2,3,\cdots,n,\cdots$ Закон распределения д. с. в. удобно задавать с помощью формулы $p_i = P{X = x_i,}, i = 1,2,3,…,n,..$ определяющей вероятность того, что в результате опыта с. в. $X$ примет значение $x_i$. Для д. с. в. $X$ закон распределения может быть задан в виде таблицы, распределения:

Множ.	-	-	-	-	-
$X$	$x_1$	$x_2$	…	$x_n$	…
$P$	$p_1$	$p_2$	…	$p_n$	…

где первая строка содержит все возможные значения (обычно в порядке возрастания) с. в., а вторая — их вероятности. Такую таблицу называ­ют рядом распределения.

Так как события ${X = x_1}$, ${X = x_2} …$ несовместны и образуют полную группу, то сумма их вероятностей равна единице т. е. $\sum_{i}p_i=1$

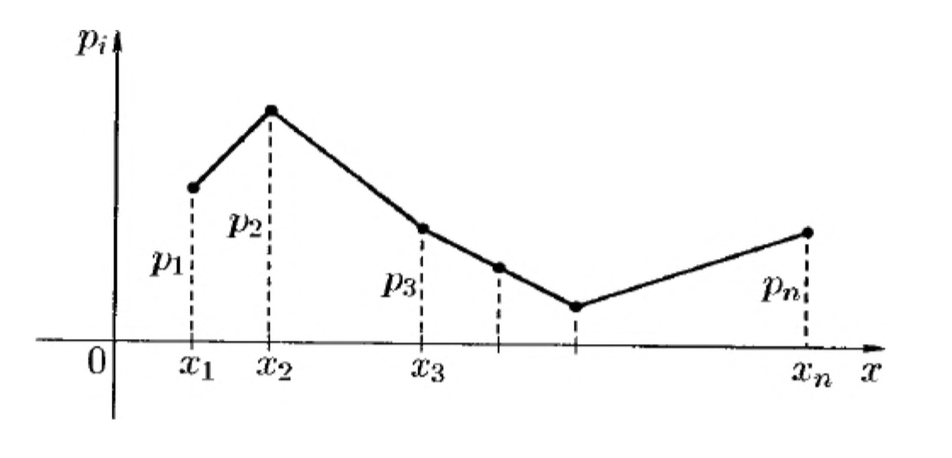
Многоугольник (полигон) распределения

Закон распределения д. с. в. можно задать графически, если на оси абсцисс отложить возможные значения с. в., а на оси ординат — вероят­ности этих значений. Ломаную, соединяющую последовательно точки $(x_1,p_1),(x_2,p_2),\cdots$ называют многоугольником (или полигоном) распределения (см. рис. 17).

Дискретная случайная величина

Случайная величина $X$ дискретна, если существует конечное или счетное множество чисел $x_1,x_2,\cdots$ таких, что $P{X = x_i} p_i > О (i = 1,2,…)$ и $p_i + p_2 + p_3 + … = 1$.

Определим математические операции над дискретными с. в.

Суммой (разностью, произведением) д. с. в. $X$, принимающей зна­чения $x_i$ с вероятностями $p_i = P{X = x_i}, i = 1,2,…, n$ и д. с. в. $Y$, при­ нимающей значения $y_j$ с вероятностями $p_j = P{Y = y_j}, j = 1,2,…,m$, называется д. с. в. $Z = X + Y (Z = X - Y, Z = X \cdot У)$, принимающая значения $z_{ij}=x_i+y_j (z_{ij}=x_i-y_j,z_{ij}=x_i\cdot y_j)$ с вероятностями $p_{ij}=P{X=x_i, Y=y_j}$ = для всех указанных значений $i$ и $j$. В случае совпадения некоторых сумм $x_i+y_j$ (разностей $x_i-y_j$, произведений $x_iy_j$) соответствующие вероятности складываются.

Дискретная случайная величина

Произведение д. с. в. на число с называется д. с. в. с $X$, принимающая значения $cx_i$, с вероятностями $p_i=P{x=x_i}$.

Две д.с.в. $X$ и $Y$ называются независимыми, если события ${X=x_i}=A-i$ и ${Y=y_j}=B_j$ независимы для любых $i=1,2,\cdots, n; j=1,2,\cdots, m$ т.е.

\[P\{X=x_i; Y=y_j\}=P\{X=x_i\}\cdot P\{Y=y_j\}\]

В противном случае с. в. называются зависимыми. Несколько с. в. на­ зываются взаимно независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины.

Функция распределения случайной величины

Очевидно, ряд распределения с. в. может быть построен только для д. с. в.; для н. с. в. нельзя даже перечислить все ее возможные значения.

Для характеристики поведения н. с. в. целесообразно использовать вероятность события ${X < x}$ (а не ${X = x}$), где $x$ — некоторое дей­ ствительное число. С точки зрения практики нас мало интересует собы­ тие, состоящее, например, в том, что лампочка проработает ровно 900 часов, т. е. $X = 900$. Более важным является событие вида ${X < 900}$ (или ${X > 900}$). Такое событие имеет ненулевую вероятность; при из­ менении х вероятность события ${X < x}$ в общем случае будет менять­ся. Следовательно, вероятность $Р{ X < x}$ является функцией от $x$.

Универсальным способом задания закона распределения вероятно­ стей, пригодным как для дискретных, так и для непрерывных случай­ных величин, является ее функция распределения, обозначаемая $F_X(x)$ (или просто $F(x)$, без индекса, если ясно, о какой с. в. идет речь).

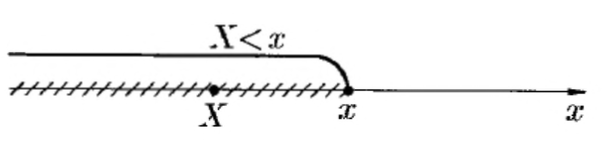
Функцией распределения с. в. $X$ называется функция $F(x)$, которая для любого числа х Е R равна вероятности события ${X < x}$.

Таким образом, по определению

\[F(x)=P\{X<x\}\]

т.е.

\[F(x)=P\{\omega: X(\omega)<x\}\]

Функцию $F(x)$ называют также интегральной функцией распределения. Геометрически равенство можно истолковать так: $F(x)$ есть вероятность того, что с. в. $X$ примет значение, которое изображается на числовой оси точкой, лежащей $x$ .т, т. е. случайная точка $X$ попадет в интервал $(-\infty, x)$

Свойства функции распределения

Функция распределения обладает следующими свойствами:

1. $F(x)$ ограничена, т. е. \(0\le F(x)\le 1\)
2. $F(x)$ — неубывающая функция на $R$, т.е. если $x_1 > x_2$, то \(F(x_2)\ge F(x_1)\)
3. $F(x)$ обращает в ноль на минус бесконечности и равна единице в плюс: бесконечности, т. е. \(F(-\infty)=0\qquad F(+\infty)=1\)
4. Вероятность попадания с. в. $X$ в промежуток $[а, b)$ равна прираще­ нию ее функции распределения на этом промежутке, т. е. \(P\{a\le X < b\}=F(b)-F(a)\)
5. $F(x)$ непрерывна слева, т. е. \(\lim_{x\to x_0-0}F(x)=F(x_0)\)

Непрерывная случайная величина

С помощью функции распределения можно вычислить вероятность события ${X \ge x}$:

\[P\{X\ge x\}=1-F(x)\]

Можно дать более точное определение н. с. в.

Случайную величину $X$ называют непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

для н. с. в. справедливы равенства

\[P\{a\le x<b\}=P\{a<x<b\}=P\{a\le x\le b\}=P\{X\in(x,b]\}\]

Функция распределения дискретной случайной величины

Функция распределения д. с. в. имеет вид

\[F(x)=\sum_{x_i<x}p_i\]

Здесь суммирование ведется по всем $i$, для которых $x_i<x$.

Плотность распределения вероятностей

Плотностью распределения вероятностей (плотностью распреде­ ления, плотностью вероятностей или просто плотностью) непрерыв­ ной случайной величины X называется производная ее функции рас­пределения.

Обозначается плотность распределения н.с. в. $X$ через $f_X(x)$ (или $p_X(x)$) или просто $f(x)$ (или $p(x)$), если ясно о какой с. в. идет речь.

Таким образом, по определению

\[f(x)=F'(x)\]

Функцию $f(x)$ называют также дифференциальной функцией распреде­ ления; она является одной из форм закона распределения случайной величины, существует только для непрерывных случайных величин.

Установим вероятностный смысл плотности распределения. Из определения производной следует

\[f(x)=\lim_{\Delta x\to 0}\frac{\Delta F(x)}{\Delta x}=\lim_{\Delta x\to 0}\frac{F(x+\Delta x-F(x))}{\Delta x}\]

Но согласно формуле $P{a\le X<b}=F(b)-F(a)$

\[F(x+\Delta x)-F(x)=P\{x\le X<x+\Delta x\}\]

Отношение $\frac{x\le X<x+\Delta x}{\Delta x}$ представляет собой среднюю вероятность, которая приходится на единицу длины участка $[x,x+\Delta x]$, т.е. среднюю плотность распределения вероятности. Тогда

\[f(x)=\lim_{\Delta x\to 0}\frac{P\{x\le X< x+\Delta x\}}{\Delta x}\]

т. е. плотность распределения есть предел отношения вероятности по­ падания с.в.в промежуток $[x;x+\Delta x)$ к длине $\Delta x$ этого промежутка, когда $\Delta x$ стремится к нулю.

Из равенства следует, что

\[P\{x\le X<x+\Delta x\}\approx f(x)\Delta x\]

То есть плотность вероятности определяется как функция $f(x)$, удо­влетворяющая условию $P{x \le X < x + { \rm d} x} \approx f(x) { \rm d}x$; выражение $f(x) { \rm d}x$ называется элементом вероятности.

Отметим, что плотность $f(x)$ аналогична таким понятиям, как плотность распределения масс на оси абсцисс или плотность тока в теории электричества.

Свойства плотности распределения

Плотность распределения обладает следующими свойствами:

1. $f(x)$ неотрицательная, т.е. \(f(x)\ge 0\)
2. Вероятность попадания н.с. в. в промежуток $[а; b]$\ равна определенному интегралу от ее плотности в пределах от $а$ до $b$, т. е. \(Р\{a\le X \le b\}= \int_a^b f(x) { \rm d}x\)
3. Функция распределения н. с. в. может быть выражена через ее плотность вероятности по формуле \(F(x)=\int_{-\infty}^xf(t) { \rm d}t\)
4. Условие нормировки: несобственный интеграл от плотности веро­ ятности н.с. в. в бесконечных пределах равен единице, т. е.

\[\int_{-\infty}^\infty f(x) {\rm d}x=1\]

Лекция 3 Числовые характеристики случайных величин

Числовые характеристики случайных величин

Закон распределения полностью характеризует случайную величи­ ну. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, характеризующие отдельные существенные свойства (черты) закона распределения с. в. Такие чи­ сла принято называть числовыми характеристиками с. в.

Важнейшими среди них являются характеристики положения: ма­ тематическое ожидание (центр распределения с. в.), мода» медиана; ха­ рактеристики рассеяния: дисперсия (отклонение значений с. в. от ее центра)» среднее квадратическое отклонение.

Математическое ожидание дискретной случайной величины

Математическим ожиданием (или средним значением) д.с. в. $X$, имеющей закон распределениям $p_i=Р{X = x_i}, i — 1,2,3,…, n$, назы­ вается число, равное сумме произведений всех ее значений на соответ­ ствующие им вероятности.

Математическое ожидание (сокращенно: м. о.) обозначается через $MX$ (или: $M[X]$, $M(X)$, $EX$, $m_X$, $a_X$).

Таким образом, по определению

\[MX=\sum_{i=1}^nx_i\cdot p_i\]

Если число возможных значений с. в. X бесконечно (счетно), то

\[MX=\sum_{i=1}^\infty x_i\cdot p_i\]

причем ряд в правой части предполагается сходящимся (в противном случае с. в. X не имеет м. о.).

Вероятностный смысл математического ожидания

Вероятностный смысл математического ожидания состоит в том, п что оно является средним значением с. в. Действительно, т. к. $\sum_{i=1}^n p_i=1$, то

\[MX=\sum_{i=1}^n=\frac{\sum_{i=1}^n x_ip_i}{\sum_{i=1}^n p_i}=x_{среднее}\]

Математическое ожидание дискретной случайной величины

Значение математического ожидания удовлетворяет следующему неравенству:

\[\min\{x_i\}\le M(X)\le\max\{x_i\}\]

Для вычисления математического ожидания достаточно знать закон распределения случайной величины.

Математическое ожидание непрерывной случайной величины

Математическим ожиданием п. с. в. $X$ с плотностью вероятности $f(x)$, называется число

\[MX=\int_{-\infty}^\infty x \cdot f(x) {\rm d}x\]

Интеграл в правой части равенства предполагается абсолютно сходящимся, т. е.

\[MX=\int_{-\infty}^\infty \lvert x\rvert \cdot f(x) {\rm d}x\lt \infty\]

(в противном случае н.с. в. $X$ не имеет м.о.).

Свойства математического ожидания

1. Математическое ожидание постоянной равно самой этой постоян­ ной, т. е.

\[Mc=c\]

1. Постоянный множитель выносится за знак м.о., т. е.

\[M(cX)=cMX\]

1. М.о. суммы с. в. равно сумме их м.о., т. е.

\[M(X+Y)=MX+MY\]

1. М. о. отклонения с. в. от ее м. о. равно нулю, т. е.

\[M(X-MX) = 0\]

1. М.о. произведения независимых с.в. равно произведению их м.о., т. е. если $X$ и $Y$ независимы, то

\[M(X\cdot Y)=MX\cdot MY\]

Дисперсия случайной величины

Дисперсией (рассеянием) с. в. $X$ называется математическое ожи­ дание квадрата ее отклонения от своего математического ожидания.

Обозначается дисперсия через $DX$ (или $D[X]$, $D_X$, $D(X)$). Таким образом, по определению

\[DX=M(X-MX)^2\]

или $DX=MX^2$, или $DX=M(X-m_X)^2$. Дисперсия характеризует разброс значений с. в. X относительно ее м. о. Из определения диспер­сии следуют формулы для ее вычисления:

\[DX = \sum_i(x_i-MX)^2\cdot p_i \ -\ для\ д.с.в.\ X\] \[DX=\int_{-\infty}^{+\infty}(x-MX)^2\cdot f(x) {\rm d}x \ -\ для\ н.с.в.\ X\]

Дисперсия случайной величины

На практике дисперсию с. в. удобно находить по формуле

\[DX=MX^2-(MX)^2\] \[D(X)=M(X^2)-(M(X))^2=\sum_{i=1}^n x_i^2 p_i-(M(X))^2=x_1^2\cdot p_1+x_2^2\cdot p_2+\cdots+x_n^2\cdot p_n-(M(X))^2\]

Доказательство:

\[\begin{split} DX=&M(X^2-2X\cdot MX+(MX)^2)\\ =&MX^2-M(2X\cdot MX)+M(MX)^2\\ =&MX^2-2MX\cdot MX+(MX)^2\\ =&MX^2-(MX)^2\\ \end{split}\]

Свойства дисперсии

1. Дисперсия постоянной равна нулю, т. е.

\[Dc=0\]

1. Постоянный множитель можно выносить за знак дисперсии, возве­ дя его в квадрат, т. е.

\[DcX=c^2DX\]

1. Дисперсия суммы независимых с. в. равна сумме их дисперсий, т.е. если X и Y независимы, то

\[D(X+Y)=DX+DY\]

1. Дисперсия с. в. не изменится, если к этой с. в. прибавить постоян­ ную, т, е.

\[D(X+c)=DX\]

1. Если с. в. $X$ и $Y$ независимы, то

\[D(XY)=MX^2+MY^2-(MX)^2\cdot(MY)^2\]

Свойства дисперсии

Пояснение. Случайные величины $X$ и $Y$ называются неза­висимыми тогда и только тогда, когда случайные события ${X = x_i}$ и ${Y = y_j}$ при любых $i$ и $j$ являются независимыми.

Из данного определения следует, что при любых $i$ и $j$ вероят­ность события ${X = x_i}$ не зависит от того, произошло событие ${Y = y_j}$ или нет. Другими словами, независимые случайные ве­личины $X$ и $Y$ не могут влиять друг на друга, взаимовлияние от­ сутствует.

Среднее квадратическое отклонение

Дисперсия $DX$ имеет размерность квадрата с. в, $X$, что в сравни­ тельных целях неудобно. Когда желательно, чтобы оценка разброса (рассеяния) имела размерность с. в., используют еще одну числовую характеристику — среднее квадратическое отклонение (сокращенно: с. к. о.).

Средним квадратическим отклонением или стандартным откло­ нением с. в. $X$ называется квадратный корень из ее дисперсии, обозна­чают через $\sigma_X$ (или $\sigma X$, $\sigma[Х]$, $\sigma$). Таким образом, по определению

\[\sigma_X=\sqrt{DX}\]

Из свойств дисперсии вытекают соответствующие свойства с. к. о.: $\sigma c=0, \sigma_{cX}=\lvert c\rvert\sigma_X,\sigma(c+X)=\sigma_X$

Стандартная случайная величина

Для изучения свойств случайного явления, независящих от выбо­ ра масштаба измерения и положения центра группирования, исходную случайную величину $X$ приводят к некоторому стандартному виду: ее центрируют,т.е.записываютразность $X-MX$ (геометрическиозна­ чает, что начало координат переносится в точку с абсциссой, равной м. о.), затем делят на с. к. о. $\sigma_X$

Случайную величину $Z=\frac{X-MX}{\sigma_X}$ называют стандартной слу­чайной величиной. Ее м. о. равно 0, а дисперсия равна 1. Действительно,

\[MZ=M(\frac{X-MX}{\sigma_X})=\frac{1}{\sigma_X}M(X-MX)=0\] \[DZ=\frac{1}{\sigma^2_X}D(X-MX)=\frac{DX}{\sigma^2_X}=\frac{DX}{DX}=1\]

То есть $Z$ — центрированная ($MZ = 0$) и нормированная. ($DZ = 1$) случайная величина.

Моменты случайной величины

Математическое ожидание и дисперсия являются частными случа­ ями следующих более общих понятий — моментов с. в.

Начальным моментом порядка $k$ с. в. $X$ называется м.о. $k$-й сте­пени этой величины, обозначается через $\alpha_k$

Таким образом, по определению

\[\alpha_k=M(X^k)\]

Для д. с. в. начальный момент выражается суммой:

\[a_k=\sum_i x_i^k\cdot p_i\]

а для н. с. в. — интегралом:

\[\alpha_k=\int_{-\infty}^\infty x^k\cdot f(x){\rm d}x\]

В частности, $\alpha_1=MX$, т.е. начальный момент 1-го порядка есть м.о.

Центральный момент

Центральным моментом порядка $k$ с. в. $X$ называется м. о. вели­чины $(X — MX)^k$. обозначается через $\mu_k$.

\[\mu_k=M(X-MX)^k\]

В частности, $\mu_2=DX$, т. е. центральный момент 2-го порядка есть дисперсия; $\mu_1=M(X-MX)=0$ (см. свойство 4 м. о.).

Для д. с. в.:

\[\mu_k=\sum_i(x_i-MX)^k\cdot p_i\]

а для и. с. в.:

\[\mu_k=\int_{-\infty}^\infty(x-MX)^k\cdot f(x){\rm d}x\]

Производящая функция

Нахождение важнейших числовых характеристик д. с. в. с целыми неотрицательными значениями удобно производить с помощью произ­ водящих функций.

Пусть д. с. в. $X$ принимает значения $0,1,2,\cdots,k,\cdots$ с вероятностями $p_0,p_1,p_2,\cdots,p_k=P{X=k},\cdots$

Производящей функцией для д. с. в. $X$ называется функция вида

\[\varphi(z)=\sum_{k=0}^\infty p_k\cdot z^k=p_0+p_1z+p_2z^2+\cdots\]

где $z$ -— произвольный параметр, $0 \lt z \le 1$.

Отметим, что коэффициентами степенного ряда являются вероятности закона распределения д. с. в. $X$

Производящая функция

Дифференцируя по $z$ производящую функцию, получим

\[\varphi'(z)=\sum_{k=0}^\infty k\cdot p_k\cdot z^{k-1}\]

Тогда

\[\varphi'(1)=\sum_{k=0}^\infty k\cdot p_k=MX=\alpha_1\]

т.е.

\[\alpha_1=MX=\varphi'(1)\]

Взяв вторую производную функции и положив в ней 2 = 1, полу­чим:

\[\varphi''(z)=\sum_{k=0}^\infty k(x-1)\cdot p_k\cdot z^{k-2}\] \[\varphi''(1)=\sum_{k=0}^\infty k^2\cdot p_k-\sum_{k=0}^\infty k\cdot p_k=\alpha_2-\alpha_1\]

где $\alpha_2$ и $\alpha_1$ — начальные моменты соответственно 2-го и 1-го порядков ($\alpha_2=MX^2$, $\alpha_1=MX$). Тогда $DX=MX^2-(MX)^2=\alpha_2-\alpha_1^2=(\alpha_2-\alpha_1)+\alpha_1-\alpha_1^2=\varphi’‘(1)+\varphi’(1)-(\varphi’(1))^2$ т. e.

\[DX=\varphi''(1)+\varphi'(1)-(\varphi'(1))^2\]

Биноминальный закон распределения

Дискретная с. в. $X$ имеет биномиальное распределение (или рас­пределена по биномиальному закону), если она принимает значения $0,1,2,3$, с вероятностями:

\[p_m=P(X=m)=C_n^mp^mq^{n-m}\]

где $0 \lt p < 1, q = 1 - р, m = 0,1,\cdots, n.$

Случайная величина X , распределенная по биномиальному закону, является числом успехов с вероятностью р в схеме Бернулли проведе­ ния п независимых опытов.

Если требуется вычислить вероятность «не менее т успехов в $n$ независимых опытах» т. е $P{X\ge m}$, то имеем: $P_m=P{X\ge m}=P{X=m}+P{X=m+1}+\cdots+P{X=n}$. Вероятность $P_m$ бывает удобно находить через вероятность противоположного события: $P_m=P{X\ge m}=1-P{X\lt m}$; та из двух формул лучше, где меньше слагаемых.

Ряд распределения д. с. в. X, имеющей биномиальное распределе­ние, имеет вид:

$X=m$	0	1	2	…	m	…	n
$p_m=P{X=m}$	$q^n$	$C_n^1p^1q^{n-1}$	$C_n^2p^2q^{n-2}$	…	$C_n^mp^mq^{n-m}$	…	p^n

Контроль:

\[\sum_{m=0}^n=(p+q)^n=1\]

Функция распределения с. в. X , распределенной по биномиальному закону, имеет вид:

\[F(x)=\begin{cases} 0\quad при\ x\le 0\\ \sum_{m\lt x}C_n^mp^mq^{n-m},\quad при\ 0\lt x\le n\\ 1,\quad при\ n\lt x\\ \end{cases}\]

Найдем числовые характеристики этого распределения. Производящей функцией биномиального распределения является

\[\varphi(x)=\sum_{m=0}^nC_n^mp^mq^{n-m}z^m=\sum_{m=0}^nC_n^m(pz)^mq^{n-m}=(q+pz)^n\]

т. е. $\varphi(z)=(q+pz)^n$. Тогда

\[\varphi'(z)=n(q+pz)^{n-1}p,\qquad\varphi''(z)=n(n-1)p^2(q+pz)^{n-2}\] \[MX=\varphi'(1)=np\] \[DX=\varphi''(1)+\varphi'(1)-(\varphi'(1))^2=n(n-1)p^2+np-n^2p^2=npq\] \[MX=np,\qquad DX=npq\]

Распределение Пуассона

Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: $0,1,2,\cdots,m,\cdots$ (счетноемножествозна­ чений), а соответствующие вероятности выражаются формулой Пуас­сона

\[p_m=P\{X=m\}=\frac{a^m\cdot e^{-a}}{m!}\]

где

• $m=0,1,2,\cdots$
• $a$ — параметр.

Распределение Пуассона является предельным для биномиального, когда $n\to \infty$ и $p\to0$ так, что $np=a$, — постоянно. Примерами слу­чайных величин, имеющих распределение Пуассона, являются: число вызовов на телефонной станции за время $t$ число опечаток в большом тексте; число бракованных деталей в большой партии; число $\alpha$-частиц, испускаемых радиоактивным источником, и т. д. При этом считается, что события появляются независимо друг от друга с постоянной сред­ней интенсивностью, характеризующейся параметром $a=nр$.

Случайная величина $X$, распределенная по закону Пуассона, имеет следующий ряд распределения

$X=m$	0	1	2	…	m	…
$p_m	$e^{-a}$	$\frac{a\cdot e^{-a}}{1!}$	$\frac{a^2\cdot e^{-a}}{2!}$	…	$\frac{a^m\cdot e^{-a}}{m!}$	…

Контроль:

\[\sum_{m=0}^\infty\frac{a^m\cdot e^{-a}}{m!}z^m=e^{-a}\sum_{m=0}^\infty\frac{(az)^m}{m!}=e^{-a}\cdot e^{az}=e^{a(z-1)}\]

т.е. $\varphi(z)=e^{a(z-1)}$. Тогда $\varphi’(z)=a\cdot e^{a(z-1)}$, $\varphi’‘(z)=a^2\cdot e^a(z-1)$. Стало быть, $MX=\varphi’(1)=a$, $DX=\varphi’‘(1)-\varphi’(1)-(\varphi’(1))^2=a^2+a-a^2=a$

\[MX=DX=a\]

Геометрическое распределение

Дискретная с. в. $X$ имеет геометрическое распределение, если ее возможные значения: 1,2,3,4,…, а вероятности этих значений:

Лекция 4